| Step | Hyp | Ref
| Expression |
|---|
| 1 | | ltexnqi 7217 |
. . . . 5
    
             |
| 2 | 1 | adantl 275 |
. . . 4
            
   
    
            |
| 3 | | subhalfnqq 7222 |
. . . . . 6
                  |
| 4 | 3 | ad2antrl 481 |
. . . . 5
                 
                         
      |
| 5 | | archrecnq 7471 |
. . . . . . 7
                   ![] ]](rbrack.gif)      |
| 6 | 5 | ad2antrl 481 |
. . . . . 6
                  
                        
                       ![] ]](rbrack.gif)      |
| 7 | | simpllr 523 |
. . . . . . . . . 10
                  
                        
              |
| 8 | 7 | adantr 274 |
. . . . . . . . 9
        
                                                            ![] ]](rbrack.gif)            |
| 9 | | simplrl 524 |
. . . . . . . . . 10
                  
                        
              |
| 10 | 9 | adantr 274 |
. . . . . . . . 9
        
                                                            ![] ]](rbrack.gif)            |
| 11 | | simplrr 525 |
. . . . . . . . . 10
                  
                        
                  |
| 12 | 11 | adantr 274 |
. . . . . . . . 9
        
                                                            ![] ]](rbrack.gif)                |
| 13 | | simplrl 524 |
. . . . . . . . 9
        
                                                            ![] ]](rbrack.gif)            |
| 14 | | simplrr 525 |
. . . . . . . . 9
        
                                                            ![] ]](rbrack.gif)                |
| 15 | | simprl 520 |
. . . . . . . . 9
        
                                                            ![] ]](rbrack.gif)            |
| 16 | | simprr 521 |
. . . . . . . . 9
        
                                                            ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)      |
| 17 | 8, 10, 12, 13, 14, 15, 16 | caucvgprprlemloccalc 7492 |
. . . . . . . 8
        
                                                            ![] ]](rbrack.gif)                           ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                           |
| 18 | | simplrl 524 |
. . . . . . . . . . . . 13
            
   
    
    |
| 19 | 18 | ad3antrrr 483 |
. . . . . . . . . . . 12
        
                                                            ![] ]](rbrack.gif)            |
| 20 | | nnnq 7230 |
. . . . . . . . . . . . . 14
            ![] ]](rbrack.gif)     |
| 21 | 20 | ad2antrl 481 |
. . . . . . . . . . . . 13
        
                                                            ![] ]](rbrack.gif)              ![] ]](rbrack.gif)     |
| 22 | | recclnq 7200 |
. . . . . . . . . . . . 13
        ![] ]](rbrack.gif)              ![] ]](rbrack.gif)   
  |
| 23 | 21, 22 | syl 14 |
. . . . . . . . . . . 12
        
                                                            ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)      |
| 24 | | addclnq 7183 |
. . . . . . . . . . . 12
                ![] ]](rbrack.gif)   
               ![] ]](rbrack.gif)       |
| 25 | 19, 23, 24 | syl2anc 408 |
. . . . . . . . . . 11
        
                                                            ![] ]](rbrack.gif)                    ![] ]](rbrack.gif)       |
| 26 | | nqprlu 7355 |
. . . . . . . . . . 11
              ![] ]](rbrack.gif)         
               ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)           |
| 27 | 25, 26 | syl 14 |
. . . . . . . . . 10
        
                                                            ![] ]](rbrack.gif)            
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)           |
| 28 | | nqprlu 7355 |
. . . . . . . . . . 11
           ![] ]](rbrack.gif)   
    
            ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)          |
| 29 | 23, 28 | syl 14 |
. . . . . . . . . 10
        
                                                            ![] ]](rbrack.gif)            
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)          |
| 30 | | addclpr 7345 |
. . . . . . . . . 10
                     ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                          ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                              ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)           |
| 31 | 27, 29, 30 | syl2anc 408 |
. . . . . . . . 9
        
                                                            ![] ]](rbrack.gif)                           ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)           |
| 32 | | simplrr 525 |
. . . . . . . . . . 11
            
   
    
    |
| 33 | 32 | ad3antrrr 483 |
. . . . . . . . . 10
        
                                                            ![] ]](rbrack.gif)            |
| 34 | | nqprlu 7355 |
. . . . . . . . . 10
          
        
      |
| 35 | 33, 34 | syl 14 |
. . . . . . . . 9
        
                                                            ![] ]](rbrack.gif)            
        
      |
| 36 | | caucvgprpr.f |
. . . . . . . . . . . 12
          |
| 37 | 36 | ad5antr 487 |
. . . . . . . . . . 11
        
                                                            ![] ]](rbrack.gif)              |
| 38 | 37, 15 | ffvelrnd 5556 |
. . . . . . . . . 10
        
                                                            ![] ]](rbrack.gif)                |
| 39 | | ltrelnq 7173 |
. . . . . . . . . . . . . 14
        |
| 40 | 39 | brel 4591 |
. . . . . . . . . . . . 13
           ![] ]](rbrack.gif)                ![] ]](rbrack.gif)           |
| 41 | 40 | simpld 111 |
. . . . . . . . . . . 12
           ![] ]](rbrack.gif)               ![] ]](rbrack.gif)      |
| 42 | 41 | ad2antll 482 |
. . . . . . . . . . 11
        
                                                            ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)      |
| 43 | 42, 28 | syl 14 |
. . . . . . . . . 10
        
                                                            ![] ]](rbrack.gif)            
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)          |
| 44 | | addclpr 7345 |
. . . . . . . . . 10
             
            ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                 
    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)           |
| 45 | 38, 43, 44 | syl2anc 408 |
. . . . . . . . 9
        
                                                            ![] ]](rbrack.gif)              
    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)           |
| 46 | | ltsopr 7404 |
. . . . . . . . . 10
  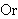  |
| 47 | | sowlin 4242 |
. . . . . . . . . 10
    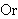          
            ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                                                     ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                   
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                                  
            ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                             |
| 48 | 46, 47 | mpan 420 |
. . . . . . . . 9
         
            ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                                                     ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                   
            ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)              
                   
            ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                             |
| 49 | 31, 35, 45, 48 | syl3anc 1216 |
. . . . . . . 8
        
                                                            ![] ]](rbrack.gif)               
            ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)              
                   
            ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                             |
| 50 | 17, 49 | mpd 13 |
. . . . . . 7
        
                                                            ![] ]](rbrack.gif)               
            ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                            |
| 51 | 19 | adantr 274 |
. . . . . . . . . 10
                
   
                        
                        ![] ]](rbrack.gif)             
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         
    |
| 52 | | simplrl 524 |
. . . . . . . . . . 11
                
   
                        
                        ![] ]](rbrack.gif)             
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         
    |
| 53 | | simpr 109 |
. . . . . . . . . . . 12
                
   
                        
                        ![] ]](rbrack.gif)             
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         
                   ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         |
| 54 | | ltaprg 7427 |
. . . . . . . . . . . . . 14
        
           
        
    |
| 55 | 54 | adantl 275 |
. . . . . . . . . . . . 13
                     
                        
                        ![] ]](rbrack.gif)             
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         
        
          
        
    |
| 56 | 42 | adantr 274 |
. . . . . . . . . . . . . . 15
                
   
                        
                        ![] ]](rbrack.gif)             
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         
         ![] ]](rbrack.gif)      |
| 57 | 51, 56, 24 | syl2anc 408 |
. . . . . . . . . . . . . 14
                
   
                        
                        ![] ]](rbrack.gif)             
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         
            ![] ]](rbrack.gif)       |
| 58 | 57, 26 | syl 14 |
. . . . . . . . . . . . 13
                
   
                        
                        ![] ]](rbrack.gif)             
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         
    
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)           |
| 59 | 38 | adantr 274 |
. . . . . . . . . . . . 13
                
   
                        
                        ![] ]](rbrack.gif)             
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         
        |
| 60 | 56, 28 | syl 14 |
. . . . . . . . . . . . 13
                
   
                        
                        ![] ]](rbrack.gif)             
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         
    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)          |
| 61 | | addcomprg 7386 |
. . . . . . . . . . . . . 14
        
               |
| 62 | 61 | adantl 275 |
. . . . . . . . . . . . 13
                     
                        
                        ![] ]](rbrack.gif)             
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         
                       |
| 63 | 55, 58, 59, 60, 62 | caovord2d 5940 |
. . . . . . . . . . . 12
                
   
                        
                        ![] ]](rbrack.gif)             
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         
                   ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                                  ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)          |
| 64 | 53, 63 | mpbird 166 |
. . . . . . . . . . 11
                
   
                        
                        ![] ]](rbrack.gif)             
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         
    
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)               |
| 65 | | opeq1 3705 |
. . . . . . . . . . . . . . . . . . 19
          
       |
| 66 | 65 | eceq1d 6465 |
. . . . . . . . . . . . . . . . . 18
            ![] ]](rbrack.gif)         ![] ]](rbrack.gif)   |
| 67 | 66 | fveq2d 5425 |
. . . . . . . . . . . . . . . . 17
               ![] ]](rbrack.gif)             ![] ]](rbrack.gif)    |
| 68 | 67 | oveq2d 5790 |
. . . . . . . . . . . . . . . 16
                  ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)     |
| 69 | 68 | breq2d 3941 |
. . . . . . . . . . . . . . 15
                     ![] ]](rbrack.gif)    
              ![] ]](rbrack.gif)      |
| 70 | 69 | abbidv 2257 |
. . . . . . . . . . . . . 14
         
             ![] ]](rbrack.gif)         
             ![] ]](rbrack.gif)      |
| 71 | 68 | breq1d 3939 |
. . . . . . . . . . . . . . 15
                   ![] ]](rbrack.gif)      
            ![] ]](rbrack.gif)        |
| 72 | 71 | abbidv 2257 |
. . . . . . . . . . . . . 14
                     ![] ]](rbrack.gif)                       ![] ]](rbrack.gif)        |
| 73 | 70, 72 | opeq12d 3713 |
. . . . . . . . . . . . 13
          
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                           ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)         |
| 74 | | fveq2 5421 |
. . . . . . . . . . . . 13
                  |
| 75 | 73, 74 | breq12d 3942 |
. . . . . . . . . . . 12
                         ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                 
               ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                |
| 76 | 75 | rspcev 2789 |
. . . . . . . . . . 11
         
               ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)               
         
            ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)               |
| 77 | 52, 64, 76 | syl2anc 408 |
. . . . . . . . . 10
                
   
                        
                        ![] ]](rbrack.gif)             
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         
         
            ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)               |
| 78 | | caucvgprpr.lim |
. . . . . . . . . . 11
               
               ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)               
                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)              
             |
| 79 | 78 | caucvgprprlemell 7493 |
. . . . . . . . . 10
              
         
            ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                |
| 80 | 51, 77, 79 | sylanbrc 413 |
. . . . . . . . 9
                
   
                        
                        ![] ]](rbrack.gif)             
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         
        |
| 81 | 80 | ex 114 |
. . . . . . . 8
        
                                                            ![] ]](rbrack.gif)               
            ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                  |
| 82 | 33 | adantr 274 |
. . . . . . . . . 10
                
   
                        
                        ![] ]](rbrack.gif)                              ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)              
                 |
| 83 | | fveq2 5421 |
. . . . . . . . . . . . . 14
                  |
| 84 | | opeq1 3705 |
. . . . . . . . . . . . . . . . . . 19
          
       |
| 85 | 84 | eceq1d 6465 |
. . . . . . . . . . . . . . . . . 18
            ![] ]](rbrack.gif)         ![] ]](rbrack.gif)   |
| 86 | 85 | fveq2d 5425 |
. . . . . . . . . . . . . . . . 17
               ![] ]](rbrack.gif)             ![] ]](rbrack.gif)    |
| 87 | 86 | breq2d 3941 |
. . . . . . . . . . . . . . . 16
                  ![] ]](rbrack.gif)   
           ![] ]](rbrack.gif)     |
| 88 | 87 | abbidv 2257 |
. . . . . . . . . . . . . . 15
         
          ![] ]](rbrack.gif)    
   
          ![] ]](rbrack.gif)     |
| 89 | 86 | breq1d 3939 |
. . . . . . . . . . . . . . . 16
                ![] ]](rbrack.gif)               ![] ]](rbrack.gif)       |
| 90 | 89 | abbidv 2257 |
. . . . . . . . . . . . . . 15
                  ![] ]](rbrack.gif)                   ![] ]](rbrack.gif)       |
| 91 | 88, 90 | opeq12d 3713 |
. . . . . . . . . . . . . 14
          
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                       ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)        |
| 92 | 83, 91 | oveq12d 5792 |
. . . . . . . . . . . . 13
            
    
          ![] ]](rbrack.gif)    
            ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)         |
| 93 | 92 | breq1d 3939 |
. . . . . . . . . . . 12
                             ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                          
            
         ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)             
        
     |
| 94 | 93 | rspcev 2789 |
. . . . . . . . . . 11
                             ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                                                      ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                           |
| 95 | 15, 94 | sylan 281 |
. . . . . . . . . 10
                
   
                        
                        ![] ]](rbrack.gif)                              ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)              
                                       ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                           |
| 96 | 78 | caucvgprprlemelu 7494 |
. . . . . . . . . 10
              
                          ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)              
             |
| 97 | 82, 95, 96 | sylanbrc 413 |
. . . . . . . . 9
                
   
                        
                        ![] ]](rbrack.gif)                              ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)              
                     |
| 98 | 97 | ex 114 |
. . . . . . . 8
        
                                                            ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                                    |
| 99 | 81, 98 | orim12d 775 |
. . . . . . 7
        
                                                            ![] ]](rbrack.gif)               
             ![] ]](rbrack.gif)                     ![] ]](rbrack.gif)                        ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                               ![] ]](rbrack.gif)                 ![] ]](rbrack.gif)                                               |
| 100 | 50, 99 | mpd 13 |
. . . . . 6
        
                                                            ![] ]](rbrack.gif)                          |
| 101 | 6, 100 | rexlimddv 2554 |
. . . . 5
                  
                        
                            |
| 102 | 4, 101 | rexlimddv 2554 |
. . . 4
                 
                                      |
| 103 | 2, 102 | rexlimddv 2554 |
. . 3
            
   
    
                  |
| 104 | 103 | ex 114 |
. 2
    
                                   |
| 105 | 104 | ralrimivva 2514 |
1
                                    |