Definition df-frind 4310

Description: Define the well-founded relation predicate. In the presence of excluded middle, there are a variety of equivalent ways to define this. In our case, this definition, in terms of an inductive principle, works better than one along the lines of "there is an element which is minimal when A is ordered by R". Because s is constrained to be a set (not a proper class) here, sometimes it may be necessary to use FrFor directly rather than via Fr. 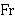(Contributed by Jim Kingdon and Mario Carneiro, 21-Sep-2021.)

Assertion

Ref	Expression
df-frind	|- ( R Fr A <-> A. sFrFor R A s )

Distinct variable groups:   R, s   A, s

Detailed syntax breakdown of Definition df-frind

Step	Hyp	Ref	Expression
1		cA	. . 3 class A
2		cR	. . 3 class R
3	1, 2	wfr 4306	. 2 wff R Fr A
4		vs	. . . . 5 setvar s
5	4	cv 1342	. . . 4 class s
6	1, 2, 5	wfrfor 4305	. . 3 wff FrFor R A s
7	6, 4	wal 1341	. 2 wff A. sFrFor R A s
8	3, 7	wb 104	1 wff ( R Fr A <-> A. sFrFor R A s )

This definition is referenced by:  freq1  4322  freq2  4324  nffr  4327  frirrg  4328  fr0  4329  frind  4330  zfregfr  4551