Description: An axiom scheme of
standard predicate calculus that emulates Axiom 5 of
[Mendelson] p. 69. The hypothesis
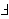   can be thought of as
emulating " can be thought of as
emulating " is not free in
is not free in  ." With this definition, the
meaning of "not free" is less restrictive than the usual
textbook
definition; for example ." With this definition, the
meaning of "not free" is less restrictive than the usual
textbook
definition; for example  would not (for us) be free in would not (for us) be free in  
 by
nfequid 1678. This theorem scheme can be proved as a
metatheorem of
Mendelson's axiom system, even though it is slightly stronger than his
Axiom 5. (Contributed by NM, 22-Sep-1993.) (Revised by Mario Carneiro,
12-Oct-2016.) (Proof shortened by Wolf Lammen,
1-Jan-2018.) by
nfequid 1678. This theorem scheme can be proved as a
metatheorem of
Mendelson's axiom system, even though it is slightly stronger than his
Axiom 5. (Contributed by NM, 22-Sep-1993.) (Revised by Mario Carneiro,
12-Oct-2016.) (Proof shortened by Wolf Lammen,
1-Jan-2018.) |