Theorem stoic2a 1417

Description: Stoic logic Thema 2 version a.

Statement T2 of [Bobzien] p. 117 shows a reconstructed version of Stoic logic thema 2 as follows: "When from two assertibles a third follows, and from the third and one (or both) of the two another follows, then this other follows from the first two."

Bobzien uses constructs such as ph, ps |- ch; in Metamath we will represent that construct as ph /\ ps -> ch.

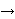This version a is without the phrase "or both"; see stoic2b 1418 for the version with the phrase "or both". We already have this rule as syldan 280, so here we show the equivalence and discourage its use. (New usage is discouraged.) (Contributed by David A. Wheeler, 17-Feb-2019.)

Hypotheses

Ref	Expression
stoic2a.1	|- ( ( ph /\ ps ) -> ch )
stoic2a.2	|- ( ( ph /\ ch ) -> th )

Assertion

Ref	Expression
stoic2a	|- ( ( ph /\ ps ) -> th )

Proof of Theorem stoic2a

Step	Hyp	Ref	Expression
1		stoic2a.1	. 2 |- ( ( ph /\ ps ) -> ch )
2		stoic2a.2	. 2 |- ( ( ph /\ ch ) -> th )
3	1, 2	syldan 280	1 |- ( ( ph /\ ps ) -> th )

Syntax hints:   -> wi 4   /\ wa 103

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-ia1 105  ax-ia3 107

This theorem is referenced by: (None)