Description: Define the conditional
operator. Read 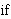 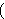     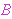 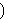 as "if as "if
 then then
 else else 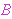 ." See iftrue 3668 and iffalse 3669 for its
values. In mathematical literature, this operator is rarely defined
formally but is implicit in informal definitions such as "let
f(x)=0 if
x=0 and 1/x otherwise." (In older versions of this database, this
operator was denoted "ded" and called the "deduction
class.") ." See iftrue 3668 and iffalse 3669 for its
values. In mathematical literature, this operator is rarely defined
formally but is implicit in informal definitions such as "let
f(x)=0 if
x=0 and 1/x otherwise." (In older versions of this database, this
operator was denoted "ded" and called the "deduction
class.")
An important use for us is in conjunction with the weak deduction
theorem, which converts a hypothesis into an antecedent. In that role,
 is a class
variable in the hypothesis and is a class
variable in the hypothesis and 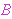 is a class
(usually a constant) that makes the hypothesis true when it is
substituted for is a class
(usually a constant) that makes the hypothesis true when it is
substituted for  . See dedth 3703 for the main part of the weak
deduction theorem, elimhyp 3710 to eliminate a hypothesis, and keephyp 3716 to
keep a hypothesis. See the Deduction Theorem link on the Metamath Proof
Explorer Home Page for a description of the weak deduction theorem.
(Contributed by NM, 15-May-1999.) . See dedth 3703 for the main part of the weak
deduction theorem, elimhyp 3710 to eliminate a hypothesis, and keephyp 3716 to
keep a hypothesis. See the Deduction Theorem link on the Metamath Proof
Explorer Home Page for a description of the weak deduction theorem.
(Contributed by NM, 15-May-1999.) |