| Step | Hyp | Ref
| Expression |
|---|
| 1 | | df-spfin 4447 |
. . 3
 Spfin Spfin  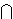     Ncfin Ncfin   
    
   Sfin Sfin        
    |
| 2 | | vex 2862 |
. . . . . . . . . . . 12
    |
| 3 | 2 | elimak 4259 |
. . . . . . . . . . 11
      Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k1c k1c     1c 1c     
  Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   |
| 4 | | el1c 4139 |
. . . . . . . . . . . . . . 15
    1c 1c   
      |
| 5 | 4 | anbi1i 676 |
. . . . . . . . . . . . . 14
     1c
1c         Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c       
         
  Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    |
| 6 | | 19.41v 1901 |
. . . . . . . . . . . . . 14
               
  Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c       
         
  Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    |
| 7 | 5, 6 | bitr4i 243 |
. . . . . . . . . . . . 13
     1c
1c         Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c       
         
  Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    |
| 8 | 7 | exbii 1582 |
. . . . . . . . . . . 12
       1c 1c         Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c                      Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    |
| 9 | | df-rex 2620 |
. . . . . . . . . . . 12
     1c
1c        Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c 

   
 1c 1c
     
  Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    |
| 10 | | excom 1741 |
. . . . . . . . . . . 12
                    Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c                      Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    |
| 11 | 8, 9, 10 | 3bitr4i 268 |
. . . . . . . . . . 11
     1c
1c        Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c 

                  Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    |
| 12 | | snex 4111 |
. . . . . . . . . . . . . 14
    
 |
| 13 | | opkeq1 4059 |
. . . . . . . . . . . . . . 15
                      |
| 14 | 13 | eleq1d 2419 |
. . . . . . . . . . . . . 14
                Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c 

    
    Sk Sk    Ins3k SIk
Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    |
| 15 | 12, 14 | ceqsexv 2894 |
. . . . . . . . . . . . 13
               
  Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c        
    Sk Sk    Ins3k SIk
Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   |
| 16 | | elin 3219 |
. . . . . . . . . . . . 13
           Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c 

         Sk Sk            Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   |
| 17 | | vex 2862 |
. . . . . . . . . . . . . . 15
    |
| 18 | 17, 2 | elssetk 4270 |
. . . . . . . . . . . . . 14
          Sk Sk      |
| 19 | | opkex 4113 |
. . . . . . . . . . . . . . . . 17
     
    |
| 20 | 19 | elimak 4259 |
. . . . . . . . . . . . . . . 16
            Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c      1 1  1 1c 1 1c          
  Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   |
| 21 | | df-rex 2620 |
. . . . . . . . . . . . . . . 16
    
 1 1  1
1c 1
1c             Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk         1 1  1 1c 1 1c         
     Ins3k SIk
Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk    |
| 22 | | elpw121c 4148 |
. . . . . . . . . . . . . . . . . . . 20
     1 1  1 1c 1 1c              |
| 23 | 22 | anbi1i 676 |
. . . . . . . . . . . . . . . . . . 19
      1 1  1
1c 1
1c               Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk  

   
                      Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk    |
| 24 | | 19.41v 1901 |
. . . . . . . . . . . . . . . . . . 19
                            Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk  

   
                      Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk    |
| 25 | 23, 24 | bitr4i 243 |
. . . . . . . . . . . . . . . . . 18
      1 1  1
1c 1
1c               Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk  

   
                      Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk    |
| 26 | 25 | exbii 1582 |
. . . . . . . . . . . . . . . . 17
        1 1  1 1c 1 1c            
  Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk  

                         
  Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk    |
| 27 | | excom 1741 |
. . . . . . . . . . . . . . . . 17
                   
    
     Ins3k SIk
Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk  

                         
  Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk    |
| 28 | 26, 27 | bitr4i 243 |
. . . . . . . . . . . . . . . 16
        1 1  1 1c 1 1c            
  Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk  

                         
  Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk    |
| 29 | 20, 21, 28 | 3bitri 262 |
. . . . . . . . . . . . . . 15
            Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c       
                      Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk    |
| 30 | | snex 4111 |
. . . . . . . . . . . . . . . . . 18
          |
| 31 | | opkeq1 4059 |
. . . . . . . . . . . . . . . . . . 19
              
    
                      |
| 32 | 31 | eleq1d 2419 |
. . . . . . . . . . . . . . . . . 18
                          Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk                      Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk    |
| 33 | 30, 32 | ceqsexv 2894 |
. . . . . . . . . . . . . . . . 17
                            Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk  

                
  Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   |
| 34 | | eldif 3221 |
. . . . . . . . . . . . . . . . 17
               
     Ins3k SIk
Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk                    
 Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
               
    Ins2k
Sk Ins2k
Sk   |
| 35 | | snex 4111 |
. . . . . . . . . . . . . . . . . . . 20
    
 |
| 36 | 35, 12, 2 | otkelins3k 4256 |
. . . . . . . . . . . . . . . . . . 19
               
    Ins3k
SIk Ins3k
SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 

    
     SIk SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c   |
| 37 | | vex 2862 |
. . . . . . . . . . . . . . . . . . . 20
    |
| 38 | 37, 17 | opksnelsik 4265 |
. . . . . . . . . . . . . . . . . . 19
          
 SIk SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 

    
   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c   |
| 39 | 37, 17 | srelk 4524 |
. . . . . . . . . . . . . . . . . . 19
          Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Sfin
Sfin       |
| 40 | 36, 38, 39 | 3bitri 262 |
. . . . . . . . . . . . . . . . . 18
               
    Ins3k
SIk Ins3k
SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Sfin
Sfin       |
| 41 | 35, 12, 2 | otkelins2k 4255 |
. . . . . . . . . . . . . . . . . . . 20
               
    Ins2k
Sk Ins2k
Sk          Sk Sk  |
| 42 | 37, 2 | elssetk 4270 |
. . . . . . . . . . . . . . . . . . . 20
          Sk Sk      |
| 43 | 41, 42 | bitri 240 |
. . . . . . . . . . . . . . . . . . 19
               
    Ins2k
Sk Ins2k
Sk      |
| 44 | 43 | notbii 287 |
. . . . . . . . . . . . . . . . . 18
                     Ins2k Sk Ins2k Sk       |
| 45 | 40, 44 | anbi12i 678 |
. . . . . . . . . . . . . . . . 17
                     Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
               
    Ins2k
Sk Ins2k
Sk    Sfin Sfin   
         |
| 46 | 33, 34, 45 | 3bitri 262 |
. . . . . . . . . . . . . . . 16
                            Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk  

 Sfin Sfin             |
| 47 | 46 | exbii 1582 |
. . . . . . . . . . . . . . 15
                   
    
     Ins3k SIk
Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk  

   Sfin Sfin        
    |
| 48 | | exanali 1585 |
. . . . . . . . . . . . . . 15
     Sfin
Sfin                 Sfin Sfin        
   |
| 49 | 29, 47, 48 | 3bitri 262 |
. . . . . . . . . . . . . 14
            Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c      Sfin Sfin
           |
| 50 | 18, 49 | anbi12i 678 |
. . . . . . . . . . . . 13
           Sk Sk            Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c 

   
     Sfin
Sfin             |
| 51 | 15, 16, 50 | 3bitri 262 |
. . . . . . . . . . . 12
               
  Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c             Sfin Sfin             |
| 52 | 51 | exbii 1582 |
. . . . . . . . . . 11
                    Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c       
       Sfin Sfin
            |
| 53 | 3, 11, 52 | 3bitri 262 |
. . . . . . . . . 10
      Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k1c k1c             Sfin Sfin             |
| 54 | | df-rex 2620 |
. . . . . . . . . 10
    
     Sfin Sfin                       Sfin Sfin             |
| 55 | 53, 54 | bitr4i 243 |
. . . . . . . . 9
      Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k1c k1c          Sfin Sfin            |
| 56 | 55 | notbii 287 |
. . . . . . . 8
       Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k1c k1c           Sfin Sfin        
   |
| 57 | 2 | elcompl 3225 |
. . . . . . . 8
    ∼ ∼   Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k1c k1c       Sk Sk    Ins3k SIk
Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k1c k1c  |
| 58 | | dfral2 2626 |
. . . . . . . 8
    
    Sfin
Sfin                     Sfin Sfin        
   |
| 59 | 56, 57, 58 | 3bitr4i 268 |
. . . . . . 7
    ∼ ∼   Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k1c k1c   
     Sfin Sfin            |
| 60 | 59 | abbi2i 2464 |
. . . . . 6
 ∼ ∼   Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k1c k1c      
     Sfin Sfin            |
| 61 | 60 | ineq2i 3454 |
. . . . 5
     Ncfin
Ncfin      ∼ ∼   Sk Sk    Ins3k SIk
Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k1c k1c       Ncfin
Ncfin            
   Sfin Sfin        
    |
| 62 | | inab 3522 |
. . . . 5
     Ncfin
Ncfin            
   Sfin Sfin        
   
   
 Ncfin Ncfin       
    Sfin
Sfin             |
| 63 | 61, 62 | eqtri 2373 |
. . . 4
     Ncfin
Ncfin      ∼ ∼   Sk Sk    Ins3k SIk
Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k1c k1c       Ncfin
Ncfin       
    Sfin
Sfin             |
| 64 | 63 | inteqi 3930 |
. . 3
 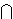   
 Ncfin Ncfin      ∼ ∼   Sk Sk    Ins3k SIk
Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k1c k1c   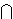   
 Ncfin Ncfin       
    Sfin
Sfin             |
| 65 | 1, 64 | eqtr4i 2376 |
. 2
 Spfin Spfin  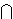     Ncfin Ncfin      ∼ ∼
  Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k1c k1c  |
| 66 | | setswithex 4322 |
. . . 4
    Ncfin Ncfin       |
| 67 | | ssetkex 4294 |
. . . . . . 7
 Sk Sk   |
| 68 | | srelkex 4525 |
. . . . . . . . . . 11
   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
  |
| 69 | 68 | sikex 4297 |
. . . . . . . . . 10
 SIk SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
  |
| 70 | 69 | ins3kex 4308 |
. . . . . . . . 9
 Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
  |
| 71 | 67 | ins2kex 4307 |
. . . . . . . . 9
 Ins2k Sk Ins2k Sk   |
| 72 | 70, 71 | difex 4107 |
. . . . . . . 8
  Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk  
 |
| 73 | | 1cex 4142 |
. . . . . . . . . 10
 1c
1c 
 |
| 74 | 73 | pw1ex 4303 |
. . . . . . . . 9
  1
1c 1
1c 
 |
| 75 | 74 | pw1ex 4303 |
. . . . . . . 8
  1 1  1
1c 1
1c 
 |
| 76 | 72, 75 | imakex 4300 |
. . . . . . 7
   Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c 
 |
| 77 | 67, 76 | inex 4105 |
. . . . . 6
  Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c 
  |
| 78 | 77, 73 | imakex 4300 |
. . . . 5
   Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k1c k1c   |
| 79 | 78 | complex 4104 |
. . . 4
 ∼ ∼   Sk Sk    Ins3k SIk Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k1c k1c   |
| 80 | 66, 79 | inex 4105 |
. . 3
     Ncfin
Ncfin      ∼ ∼   Sk Sk    Ins3k SIk
Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k1c k1c    |
| 81 | 80 | intex 4320 |
. 2
 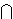   
 Ncfin Ncfin      ∼ ∼   Sk Sk    Ins3k SIk
Ins3k SIk   Nn Nn  k Nn k Nn     Ins3k Ins3k   Ins3k SIk Ins3k SIk    1c 1c  k k  
   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c  Ins2k Ins2k   Ins3k SIk ∼ Ins3k SIk ∼   Ins3k Sk Ins3k Sk  Ins2k SIk Sk Ins2k SIk Sk   k k 1 1  1 1c 1 1c  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k k 1 1  1 1  1 1c 1 1c 
 Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c   k1c k1c    |
| 82 | 65, 81 | eqeltri 2423 |
1
 Spfin Spfin   |