On the Notes on Various Proof Systems page, jcorneli asked about the state of the art in translations between various proof systems.
The good news is that there is now recognition of the need for such translations. The bad news is that most systems are still isolated islands, with no practical translation in or out yet implemented.
Here's a quote from the Flyspeck project fact sheet, speaking to the recognition that translations are important.
- As participation in the flyspeck project grows, other formal theorem proving systems have been added (Coq, Isabelle). The eventual aim will be to get the different systems to communicate meaningfully, and bring the project to a unified conclusion.
Within the HOL world, there are several successful translations. One of the more interesting is OpenTheory, which ports theorems between ProofPower/HOL, HOL4, and hol-light. A quote from that page points to difficulties with translations between more disparate systems.
- [1] Isabelle/HOL would also be desirable, but more difficult because "Isabelle offers a slightly extended type system with type classes (like group and ring)." [Nipkow, hol-info 11/9/2004]
That said, Doug Howe has had success translating HOL proofs to NuPRL, which is especially challenging because HOL uses classical logic and NuPRL constructive. See Importing Mathematics from HOL into Nuprl. However, this work can be considered a weak form of translation, as it basically just imports the statements as verified by HOL into NuPRL, rather than resulting in valid, checkable NuPRL proofs.
raph is very actively working on translations to and from Ghilbert. His Ghilbert Pax library, in particular, is designed for this purpose. See that page for more information on the underlying philosophy. Translations in both directions between Ghilbert and HOL are in the works, with encouraging early results, but still not a complete implementation.
Please add more information about other systems. My knowledge is far from encyclopedic. --raph
Metamath to Isabelle/ZF
I am working on importing Metamath theorems into Isabelle/ZF. The latest (1.2.0) release of IsarMathLib contains about 230 facts and 100 proofs from set.mm and a translation tool (written in Haskell, GPL2+).--slawekk
This is very interesting. I haven't had a chance to look at your code, but I have a number of questions from my ignorance, that I hope you don't mind answering:
- What were the major issues in making this translation?
- So far, there are no major issues. However, this is only a beginning, so there may be some difficult problems ahead. Also, I don't hope to have a fully automatic translation, some manual intervention will always be necessary for some of the proofs to be accepted by Isabelle.
- Update 03/26/2007: After translating about 1000 facts and 500 proofs I have encountered an issue with how Metamath and Isabelle/ZF treat the intersection of the empty set. In Isabelle/ZF
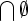 is defined as
is defined as 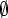 (this fact is not used in practice as all theorems about intersections assume we are intersecting a nonempty collection of sets, so the intersection of the empty set is treated as not defined). This means that Metamath's elint theorem is false in Isabelle/ZF and consequently the proofs of lots of of others that depend on it can not be directly translated. I first noticed that when trying to translate the proof of 1nn. This is quite difficult to work around. --slawekk
(this fact is not used in practice as all theorems about intersections assume we are intersecting a nonempty collection of sets, so the intersection of the empty set is treated as not defined). This means that Metamath's elint theorem is false in Isabelle/ZF and consequently the proofs of lots of of others that depend on it can not be directly translated. I first noticed that when trying to translate the proof of 1nn. This is quite difficult to work around. --slawekk- I take it you did find a workaround? I'm not sure what you did for 1nn, but I would guess that many such cases, e.g. elint, can be probably be handled by adding a hypothesis (redundant for set.mm) specifying that the intersection argument be nonempty. Anyway, there are three standards in the set theory literature, one where the intersection of the empty set is the universe, another where it is the empty set, and a third where it is left undefined. The first one tends to be used in texts that use virtual class theory, like set.mm does, and I chose it in order to prove theorems exactly as they appear in those books.
- about intersection of empty set: http://mathforum.org/library/drmath/view/62503.html
- .
- But there is a much deeper issue here, which is that there are always going to be conflicts between set.mm and Isabelle/ZF the way you are doing it, i.e. with a direct mapping of expressions, because the former uses Quine's virtual class theory and the latter doesn't. Even though virtual class terms (the capital letter variables in set.mm) behave like set variables in many instances, there is a fundamental difference in that any expression with class variables is really a theorem scheme, not a particular theorem, and corresponds to an equivalent scheme using wff variables.
- .
- There is an algorithm (outlined in Quine, and more or less explicit in Takeuti/Zaring) for converting from virtual classes to schemes involving wffs and vice-versa, and a "perfect" translator to/from Isabelle would implement this algorithm to eliminate any virtual class terms from the set.mm expression. Under this algorithm, all theorems in set.mm would have a 1-1/onto correspondence to Isabelle theorems (disregarding any limitations of wff variables in Isabelle, which I don't understand well). The algorithm involves breaking up the set.mm expression and reconstructing an equivalent scheme with wff variables. A rough idea of the algorithm, along with examples going from class terms to wff variables and back, is given in the description of abeq2. For example, A=A in set.mm is not a "generalization" of x=x, but in fact translates back and forth exactly to the propositional calculus theorem scheme phi<->phi.
- .
- Under a perfect translation, things like df-int would map to a scheme with wff variables, not a direct symbol-for-symbol replacement. Even things like df-uni, that "seem" to be exactly like Isabelle, strictly speaking also map to a wff scheme and not a symbol-for-symbol replacement. For example, the union of the universe univ is well-defined in set.mm, but not (directly) in Isabelle - but there does exist well-defined Isabelle expression that it can be translated back and forth to.
- .
- This isn't to say that you shouldn't continue what you are doing - it is fine from a practical point of view, and no matter what, the Isabelle/ZF verifier will tell you whether the translation worked. My point is that the apparent incompatibilities between the two approaches are not intrinsic - after all, they both use the same ZF axioms - but are just due to the casual approach of treating set.mm's virtual class terms as if they are variables ranging over sets. A "perfect" translator might not even be ideal in the sense you might expect - a compact class expression in set.mm might only be translatable to a long, awkward-looking wff scheme in Isabelle/ZF that would obscure the meaning from a human point of view. The main advantage would be that a completely automated translation would be possible, at least in principle. – norm 27-Mar-2007
- I take it you did find a workaround? I'm not sure what you did for 1nn, but I would guess that many such cases, e.g. elint, can be probably be handled by adding a hypothesis (redundant for set.mm) specifying that the intersection argument be nonempty. Anyway, there are three standards in the set theory literature, one where the intersection of the empty set is the universe, another where it is the empty set, and a third where it is left undefined. The first one tends to be used in texts that use virtual class theory, like set.mm does, and I chose it in order to prove theorems exactly as they appear in those books.
- Another problem is that Isabelle/ZF allows only set comprehensions that are subsets of a given set (i.e the form
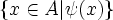 rather than
rather than 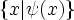 ). Also, Isabelle/ZF does not support infix notation for sets, that is
). Also, Isabelle/ZF does not support infix notation for sets, that is 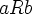 is not allowed when
is not allowed when 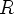 is a set. These two can be worked around quite easily so far.
is a set. These two can be worked around quite easily so far.
- Update 03/26/2007: After translating about 1000 facts and 500 proofs I have encountered an issue with how Metamath and Isabelle/ZF treat the intersection of the empty set. In Isabelle/ZF
- In particular, how did you address the differences in distinct variables? Does the Isabelle version assume "maximally distinct variables," or can you use it to prove such things as alcom with x and y unified?
- From time to time I have to change the statement of the theorem or the proof by hand. I am guessing that some of the changes I have to make are related to the disting variables problem. As for the alcom example, I just checked that the following is accepted by Isabelle/ZF
- lemma MMI_alcom: shows "
 " by auto
" by auto
- lemma MMI_alcom: shows "
- That's it for the proof. If this theorem is referenced in a proof and Isabelle does not accept this I deal with the issue on a case by case basis.
- Raph may be thinking of the case where instantiation of alcom leads to x and y being replaced by the same variable, as in this proof of A. x A. x ph → A. x ph:
1 alcom $p |- ( A. x A. x ph <-> A. x A. x ph )
2 ax-4 $a |- ( A. x A. x ph -> A. x ph )
3 1,2 sylbi $p |- ( A. x A. x ph -> A. x ph )- I'm not sure if this is the best example, since we are just re-proving an instance of ax-4. The point is that alcom couldn't be used (by Metamath) in this proof if x and y were required to be distinct. But since they aren't, Metamath is fine with this proof. A better example might be sbid, where free variable y and bound variable x in sbequ12 are replaced with the same variable for use by the proof (which might be easier to see if we replace the substitution notation by its definition df-sb throughout the proof and final theorem). – norm 23 Oct 2006
- I tried to verify
- lemma MMI_alcom1: shows "
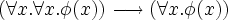 " by auto
" by auto
- lemma MMI_alcom1: shows "
- in Isabelle and it was accepted, but converted to the form "
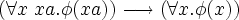 " . I guess the answer to raph's question is that all Isabelle/ZF variables are (internally) distinct. If I use the same name for two variables one of them will be renamed. This means that some core (meaning "before recnt") Metamath theorems can not be formulated in Isabelle/ZF and mean the same thing as in Metamath. I will have to modify the proofs that reference such theorems to workaround this. The experience so far suggests that this doesn't happen often. – slawekk
" . I guess the answer to raph's question is that all Isabelle/ZF variables are (internally) distinct. If I use the same name for two variables one of them will be renamed. This means that some core (meaning "before recnt") Metamath theorems can not be formulated in Isabelle/ZF and mean the same thing as in Metamath. I will have to modify the proofs that reference such theorems to workaround this. The experience so far suggests that this doesn't happen often. – slawekk- I suspected that would be the case, as it probably is with most proof languages other than Metamath. You are right that in the mainstream set.mm theorems beyond logic and early set theory, bound variables tend to be distinct, so translating those, possibly with some manual interaction, might not not be too much of a problem. However, for the long term we would want to look at how translations could be automated completely, without having to manually resolve special cases. Elsewhere I have discussed how the set.mm axioms could be reformalized for this purpose: (1) See my comments of 19-Jan-2006 and 21-Jan-2006 at mmj2Feedback about how one could go about emulating other theorem provers where all individual variables are distinct by definition. (2) Related is my 19-Jan-2006 comment on Notes on Various Proof Systems, and also my 18-Jan-2006 main comment in which that one is indented. I think that a program could be written to convert set.mm to an all-variables-are-distinct form automatically, essentially by breaking up the axioms and theorems into all possible cases (then trimming away the probably large number of unused cases that would result, if we wish). – norm 23 Oct 2006
- Let's think for a moment about possible translation the other way - from Isabelle to Metamath. This would be much more difficult and valuable project. The problem is that Isabelle does not provide a complete proof in the Metamath sense, only high level Isar scripts which are then interpreted, gaps filled by the internal Isabelle's theorem prover and the proofs discarded after deciding that they exist. Translating such Isar scripts would amount to doing the same with the internal proof language replaced by Metamath. This would require an interpreter of Isar and a theorem prover for Metamath to fill in the gaps. The moment such thing exists I would stop IsarMathLib development and start doing Metamath/Isar.
- Perhaps the Isabelle code has a debugging feature that would cause it to print out the little proofs that it is discarding – otherwise, how could you verify that the internal provers have no bugs? But if not, the only way I could see would be to intercept the internal code to make it do this, which might be a difficult task for someone who is unfamiliar with the code. – norm 25 Oct 2006
- Can your tool translate just about any set.mm theorem, or does it do just selected theorems with handholding?
- In principle it can translate just about any set.mm theorem. However, it is in an early alpha stage, so I don't expect it to translate more than 10 theorems at a time without having to modify the Haskell source to deal with some construct or syntax that is not supported yet. It doesn't translate definitions.
Presumably, the axiomatic systems are compatible enough that the constructions themselves shouldn't need much changing.
- This is precisely what is happening. I don't import directly from set.mm, I import from the output of show statement and show proof /lemmon /renumber commands. It's actually a dirty hack that works better than I expected, I think mostly because we are translating from ZF to ZF. I also don't plan to import all proofs from Metamath. I import only proofs of the theorems from recnt on, and the dependencies of those are mostly proven automatically by Isabelle. I decided to do it this way after unsuccesful attempts to prove the Metamath's axiom of replacement within Isabelle/ZF.
- What problem(s) did you encounter trying to prove Replacement? – norm
- I don't remember exactly. I typed the axiom as it was and tried if Isabelle can prove this automatically, that didn't work, then I tried to do it in small steps, that didn't work and then I gave up and decided that the farther from the fundamentals, the easier the translation. – slawekk
- What is the form of the Replacement Axiom that Isabelle uses - which hopefully you can express in the Metamath language for me? I (or some other volunteer) could try to prove set.mm's Replacement from it under Metamath, and if successful, that proof could then guide the Isabelle proof. Replacement axiom equivalents can be nontrivial to prove, and it doesn't surprise me that Isabelle (or any prover) would have trouble with it. Also, is Separation stated as a separate axiom in Isabelle, or is it derived from Replacement? – norm 23 Oct 2006
- The replacement axiom in Isabelle/ZF looks as follows:
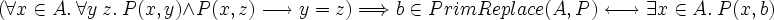
- The
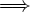 "connective" in pre-Isar Isabelle separates premises and assertions in theorems, so this axiom states that the theorem that assumes
"connective" in pre-Isar Isabelle separates premises and assertions in theorems, so this axiom states that the theorem that assumes 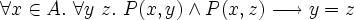
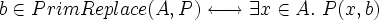
- Well, this is kind of bizarre. It seems PrimReplace is some kind of ad-hoc extra-logical device intended to represent the image of the function encoded by predicate P(x,y). On the surface, it doesn't look very elegant (giving set theory two primitives, epsilon and PrimReplace) and would seem to complicate the soundness justification of the logic. Anyway, since PrimReplace is a set, from it we could derive the existence form of Isabelle's axiom, which would almost be set.mm's axrep5 except for the antecedent. For the antecedent, note that
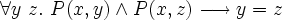
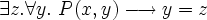
- .
- While trying to understand what PrimReplace might mean, I came up with two Metamath theorems. Theorem isarep1 shows that if we assume PrimReplace is the image of the function encoded by P(x,y), then, strangely, we can prove the conclusion of Isabelle's Axiom of Replacement using only Metamath's axioms of Extensionality and Pairing, with no reference to the Isabelle hypothesis. On the other hand, isarep2 shows that we need (Metamath's) Replacement and the hypothesis to prove the existence of the object PrimReplace, whereas in Isabelle it appears that the existence of PrimReplace is not arrived at via an axiom but is essentially "declared", simply by stating PrimReplace is of type set. I am still confused by what PrimReplace really means and how it is justified metalogically. In any case it appears we can emulate Isabelle's version in Metamath, although it still isn't clear to me why we need PrimReplace in the first place. It also isn't clear to me why Isabelle even needs set theory axioms since merely stating an object's type makes it exist, apparently. I wonder how inconsistency can be avoided…very puzzling; I'm sure there are many pieces here that I don't understand. :) norm 26 Oct 2006
- Well, this is kind of bizarre. It seems PrimReplace is some kind of ad-hoc extra-logical device intended to represent the image of the function encoded by predicate P(x,y). On the surface, it doesn't look very elegant (giving set theory two primitives, epsilon and PrimReplace) and would seem to complicate the soundness justification of the logic. Anyway, since PrimReplace is a set, from it we could derive the existence form of Isabelle's axiom, which would almost be set.mm's axrep5 except for the antecedent. For the antecedent, note that
- It's a bit over my head as I am just an Isabelle user and so far I haven't had to venture into the Isabelle/ZF fundamentals. From a practical point of view in Isabelle/ZF proofs there is no difference if one has a theorem A:
 or a theorem B:
or a theorem B: 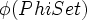 . If we have A, then we we can say in the proof "from A obtain PhiSet? where B:
. If we have A, then we we can say in the proof "from A obtain PhiSet? where B: 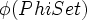 ". If we have B then we can say "from B have A:
". If we have B then we can say "from B have A:  ". It is probably the case that some stuff that corresponds to Metamath axioms is hardwired into Isabelle type system or syntax declaractions and is not called "axioms". This this why I have never had to prove explicitly that something is a wff. For example in my translation project Metamath's
". It is probably the case that some stuff that corresponds to Metamath axioms is hardwired into Isabelle type system or syntax declaractions and is not called "axioms". This this why I have never had to prove explicitly that something is a wff. For example in my translation project Metamath's 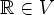 is translated (effectively) to
is translated (effectively) to  . Since "=" is an operator that takes two sets, Isabelle does "type inference" and (I assume) the meaning is preserved. The Isabelle axioms are defined in this theory file.
. Since "=" is an operator that takes two sets, Isabelle does "type inference" and (I assume) the meaning is preserved. The Isabelle axioms are defined in this theory file. - I was able to prove Metamath's axrep5 and axrep4 in Isabelle using your guidelines above. The proof document is posted here. – slawekk
- Excellent! It will be interesting to see how far the axrep4 translation can take us in Isabelle. Will it be sufficient for everything (meaning that PrimReplace is unnecessary) or will we run into an obstacle (that PrimReplace is needed to overcome)? I'll keep an eye on your progress. – norm 27 Oct 2006
I'm personally interested in translations across axiomatic systems too, but that involves many different issues. An example would be the recent work in topology and metric spaces, which can be translated into HOL, but requires imposing types, such as this one for metric spaces:
( T -> bool) * ( ( T * T ) -> real )
In set.mm, ad-hoc polymorphism is straightforward, but in HOL, a more disciplined approach is required, which uses T to represent generic polymorphism (note that 'a or 'alpha is also common notation for generic polymorphism in the ML/HOL tradition). – raph
- I think translating between different logical frameworks is much more difficult, especially if differences in type systems get in the way. I hope that the high-level language interface to the future theorem prover for Metamath will have as many types as natural for ZF (two: Set and {True,False}). --slawekk