"Inverse Proving" Project Idea
My arduous efforts to reprove hbimd resulted in a shorter proof of hbim, but no improvement of the proof for hbimd itself. As is often the case, in my experience, time spent suffering on an unsolved problem produces benefits – if one persists through the discomfort.
My latest idea is the inverse of writing code to search all of the possibilities for proving hbimd. Begin with the axioms and definitions and run code to generate all possible theorems…until a proof of hbimd is achieved. (How much CPU time this would burn through is an interesting question in its own right.)
This idea builds upon my "discovery" (which I think Norm already knew), that a Metamath RPN-format proof has two levels of structure. The "micro" RPN level includes variable hypotheses, syntax axioms in addition to the "macro" RPN level which contains only non-syntax assertions and logical hypotheses. The macro RPN proof level completely determines the Most General form of a provable assertion (AKA theorem). So, the proof of theorem a1i at the macro level is just "a1i.1 ax-1 ax-mp". And mmj2 can fill in all proof details for a1i given just those three statement labels in RPN order.
- MM Solitaire uses the "macro" level. However, that level is built into its internal (hard-coded) "database" of axioms. The power of mmj2 is that it effectively deduces the "macro" level from the "micro" level via its parser, a feature that the metamath.exe program doesn't have. – norm
To complete the idea as a project it would be necessary to figure out:
- rules for building all valid proof sequences of non-syntax assertions.
- how to eliminate redundant, repetitive sequences (and answer the question: Are non-redundant, non-repetitive sequences "interesting"?)
- how to determine appropriate logical hypotheses for generated theorems
- how to efficiently and compactly store the massive number of generated theorems for use in a) generating more theorems, and b) unification searches later. Developing an "optimal" in-memory data structure satisfying the need for inserts, direct-access retrievals and partial scans (unification searches) is a tricky project in its own right!
- how to name the generated theorems (also, should a look-up into a .mm file be performed for the benefit of humans – e.g. if "syl" is derived shouldn't we name the generated theorem "syl"?)
Here is an example of using the mmj2 Proof Assistant to build Most General theorems using the "Derive" feature:
$( <MM> <PROOF_ASST> THEOREM=a1i LOC_AFTER=?
*
1100::ax-2 |- ( ( &W2 -> ( &W4 -> &W8 ) ) -> ( ( &W2 -> &W4 ) -> ( &W2 -> &W8 ) ) )
2100::ax-2 |- ( ( ( &W2 -> ( &W4 -> &W8 ) ) -> ( ( &W2 -> &W4 ) -> ( &W2 -> &W8 ) ) )
-> ( ( ( &W2 -> ( &W4 -> &W8 ) ) -> ( &W2 -> &W4 ) )
-> ( ( &W2 -> ( &W4 -> &W8 ) ) -> ( &W2 -> &W8 ) ) ) )
100:1100,2100:ax-mp
|- ( ( ( &W2 -> ( &W4 -> &W8 ) ) -> ( &W2 -> &W4 ) )
-> ( ( &W2 -> ( &W4 -> &W8 ) ) -> ( &W2 -> &W8 ) ) )
*
4:?: |- &W1
5::ax-1 |- ( &W1 -> ( &W3 -> &W1 ) )
6:4,5:ax-mp |- ( &W3 -> &W1 )
*
h7::a1i.1 |- ph
8::ax-1 |- ( ph -> ( ps -> ph ) )
qed:7,8:ax-mp |- ( ps -> ph )
$= wph wps wph wi a1i.1 wph wps ax-1 ax-mp $.
$)
As you can see, steps 4->6 represent theorem a1i itself, and step 4's formula is "|- &W1", which indicates a mandatory stopping point since "&W1" could not be more general :-)
Steps 1100, 2100 and 100 reveal a theorem not in set.mm.
At the conclusion of the project it would be nice if estimates, formulas or bounds could be stated – such that, given axioms A1, A2, … AN involving variables v1, v2, … vN we would know how many additional variables and non-redundant, non-repetitive theorems would result – assuming, say, a maximum formula length of L. That is asking a lot, but the result feels important because the algorithm for "inverse proving" would be applicable to set.mm, ql.mm and any other valid .mm file regardless of syntax or logical assumptions -- assuming an unambiguous grammar and consistent axioms. If we were able to maximally compact(ify) the generated theorems for a given set of axioms then the task of Proof Assistanting would be much easier to code in software (utility based on the assumption that with 10 years it is quite likely that home PCs will be equipped with something like 256GB of non-volatile RAM.) Also, using this approach it would be possible to rapidly populate a .mm database from a set of syntax and logical axioms – something which is exceedingly time-consuming with the current state of the art software…
- On the Shortest
known proofs... page, all proofs with 21 or less steps were found by exhaustive generation of all possible proofs, so they are the shortest possible proofs. Greg Bush may have extended this to 23 or 25 steps, not sure, in his work that further shortened 67 proofs using computers available a decade later (and his clever algorithms). After a couple of dozen steps, though, you hit an exponential brick wall with the exhaustive approach. The longer proofs were basically the shortest ones I could find by hand, which were then shortened as much as possible by seeing if the subproofs of any of their steps could be shortened with 21-or-less-steps proofs. Greg may have used different techniques for his shorter proofs; his algorithms are something of a mystery to me, or perhaps he was allowed to peek at God's book of proofs. :) – norm 5 May 2008
- Combinatorial explosions are the number one Gotcha when writing these kinds of programs (the mmj2 hypothesis sorting prior to unification (if the input hyp order fails) is done to prevent it.) I don't know if I would be interested in actually writing this code, but writing the specs for the optimal algorithm would be interesting (especially if getting paid by the NSF <:-) My "vision" is to add each new non-repetitive, non-redundant theorem to the input list of assertions for use in generating more theorems -- and to write out the results in a .mm file. In theory the process should have checkpoint/restart, thus enabling it to utilize surplus computer power over time. (I hear what you're saying though, it is one of those wild ideas that probably is of interest only as a gedankexperiment.)
- .
- This is really a very interesting project idea. I have it stuck in my head now, like a pop song :-) Obviously, it would not require the use of mmj2, and it would be unreasonable to expect a computer scientist to do anything other than code up the project from scratch; in fact, mmj2 has built-in inefficiencies which would be problematic if one were attempting a mega-derivation effort (on the other hand, given my familiarity with my own code – I would probably use it anyway :-)
- .
- Just pondering this has given me new ideas about how to handle the Unification Search problem with a database containing 1 million assertions. One approach is to use a forest of trees where each root is the root of a parse tree – specifically, a syntax axiom node – and then building the tree for downward searching based on an input parse tree. Another approach keys off of the fact that each theorem's 'qed' step formula is an instance of another assertion's 'qed' step's formula – this provides a hierarchy which could be searched downwards, and in fact, this approach could be melded with the first approach (I think.)
- .
- One other thought, for maximum compactification – an utter necessity given a database of 1 million assertions and the need for speedy unification searches – all of the work could be done using RPN; conversion back to Metamath-standard syntax could be done at output-display generation time, if desired (mmj2 doesn't care whether the syntax is polish, infix or mixed and set.mm can easily be converted to use RPN throughout. Instead of the "( ph → ps )" formulas it would be "ph ps wi" everywhere. For a code-from-scratch project there would be some fun optimizations if the whole thing was done using RPN, perhaps with a lambda-style substitution scheme to simplify manipulations. Fun stuff, indeed!
- .
- What I think would be most interesting about this project would be trying to write the rules for determining whether or not a theorem should be generated from a candidate list of statement labels. What determines if hypotheses should be generated? What are the families of patterns that are good or bad? Obviously, a generated theorem should not be an instance of another theorem, which means that after generating a new theorem a Unification Search must be attempted. But beyond that, what would make the program decide to recreate something like hbimd, which has three hypotheses? I also like the exploratory part of the work -- for example, populating a .mm file with an initial set of theorems given an input set of assertions…perhaps interesting discoveries would result!
- --ocat 5-Mar-2008
"Inverse Proving" Project Idea -- Spin-off Ideas
1) Assume that the Inverser Prover algorithm were run for just the propositional logic axioms – for all generated theorems containing up to 5 wff variables, and eliminating redundant, repetitive assertions (somehow determining this in a useful manner.) Then, how many theorems would result? 1 million? Less?
Because here is my idea: instead of trying to add enough theorems to set.mm to make it work really well with the mmj2 Unification Search, which looks for justifying assertions for a given proof step, instead use the generated theorems "database" for the Unification Search. And then, if the justifying Ref for a step is not contained in the loaded .mm file, the generated theorem's proof would be "in-lined" into the Proof Worksheet!
So the goal is to provide a propositional logic "prover" assistant without have to hard-code logic or write a plug-in module for each input .mm database.
The other part of the problem, of finding the matching hypotheses for the given proof step – and this assumes that the user knows that only propositional proving is being performed automatically and that any higher logic must be handled manually – could also be performed using the generated theorem "database". In effect, a Unification Search would be performed for each prior proof step using each as an hypothesis and returning a set of matching assertions. Then those sets would be intersected with the set of justifying assertions for the given proof step's formula. Any remaining un-justified hypotheses would be "derived" and then the process would be repeated if necessary (which sounds tedious but really, isn't as horrible as it sounds – it is precisely what the task demands.)
2) Here is another spin-off idea, which probably would end up being needed for a solution which is capable of taking advantage of multiprocessing CPU cores with concurrent threads…
The original mmj2 "logical database" design is flawed in certain ways. One problem is that each Metamath statement gives rise to a single MObj (Metamath Object) and then references to that MObj are used throughout the rest of the code. For example, when set.mm is read in there is only one ")" object and each formula using a ")" contains a reference to that object.
This becomes a problem later during the new StepUnifier? logic which wants to store substitutions into variable hypothesis parse tree nodes -- and of course there is only one instance of each variable hypothesis. The problem is "solved" in mmj2 but only by guaranteeing non-simultaneous access to VarHyp? MObj's.
The solution is to make the new, say, "mmj3" database design adhere more closely to the true nature of the reality it is trying to model. Specifically, most input Metamath statement's MObj are really just a models, and what gets used later are specific instances of those models. For example, "ph" in one formula is not, in reality, the same "ph" that is used in another formula.
So, each formula loaded into memory will contain references to instances of MObj's. There would be one "ph" instance per assertion, I think…instead of one "ph" for the entire database. This would not require extra memory however, because as it stands now, each mmj2 parse tree consists of ParseNodes?, and the ParseNode? instances contain references to the specific MObj for the node. So what would be done is to eliminate the ParseNode? object altogether and to put the tree link data items right into instances of the syntax axioms!
--ocat 7-Mar-2008
Summary of Idea
I think this project could be called the "Auto-Loader".
Input: a .mm file containing the Var, Var Hyp, Syntax Axiom, Definition Axiom and Logical Axioms forming the foundation of your logical system.
Output: a .mm file containing the first 'n' theorems resulting from the input .mm file – with stipulations on the output theorems: a) use no more variables than are input; b) no more than twice as long as the longest input logical axiom; c) not an instance of any previous assertion (i.e. no zero-length proofs); and d) not an endless loop creating by just re-applying the same assertion over and over again (the way that a1i could be used to create endless "new" theorems); e) any logical hypotheses must be independent of each other, meaning that hypothesis m cannot be derived from hypotheses i, j, k, etc.
Note that each newly generated theorem is added to the input so that it in turn is used to generate additional theorems in combination with the previous axioms and theorems.
And, note that by generating the theorems in ascending order from shortest derivation to longest – and checking for redundancies as the work progresses – the output will automatically contain the shortest proof of each output theorem.
THEN…when the output .mm file is available it can be used as a Library by the Proof Assistant! Unification Searches will scan the library instead of the normal input .mm file (set.mm for example), and when a unifying assertion is found if the same assertion is not found in the input .mm file, the derivation is "in-lined" into the user's proof (checking that those proof step formulas are present or not in the input .mm file, multiple derivations may need to be in-lined.)
So…this idea may not work on today's computers, but the beauty of it is that it is an approach to proof assistanting which is "logic agnostic". Suppose that supporting propositional logic and the "pure" predicate logic foundations of set.mm requires a Library of 10 million theorems. That won't be a problem in the year 2017 – and here is why: a) in 2017 standard PC's will be equipped with 256GB non-volatile RAM, and b) once the Library is computed for a given set of variables, syntax and axioms, it never needs to be recomputed! So, say each theorem in the Library requires 1K and you have 10 million – that amounts to just 10GB of storage, which won't be a problem in 2017.
And, since this is logic-agnostic, the same code will work equally well for ql.mm as it does for set.mm. Or, if, say you want to add XOR to your logic syntax. Just run the Auto-Load to generate the Library and you have an initial .mm file to play with! Ditto for 3-valued logic – just input your variables, syntax, definitions and logic axioms and bada-bing, bada-boom, three days later your Library is constructed…(execution times faster in 2017 of course.)
Spin-off Idea: Maximal Compression of a .mm File
See MaximallyCompressedMetamathDatabases for updated specs.
(My Latest "Discovery")
In theory formulas on $p and the $e and $d statements associated with those $p statements are redundant and can be recreated from the proof of the $p.
Previously, in mmj2, it was shown that the $d statements for $p's can be derived from the axioms (except if the author of the .mm file has chosen to add excessively strict $d's – and, $d's for optional variables (useless) change depending on the somewhat arbitary choices of optional variables used in a proof.)
Also, it has been shown that the "ASCII shorthand" formulas can be rederived from the Syntax RPN lists (which correspond to parse trees).
And, finally, it has been shown that a Metamath proof need not contain syntax axiom and variable hypothesis labels – these details can be filled in by unification – so all that is needed to specify a Metamath proof is an RPN list of the logical assertions and logical hypotheses used in the proof.
So, the ultimate in .mm file compression is to eliminate formulas on $p statements and on the $d/ $e statements associated with those $p's. Formulas would be used only for 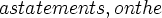 e's and $d's associated with those $a statements, and any $f statements. And, for maximum speed of parsing, Syntax RPN "proofs" would be used instead of "ASCII shorthand", except on the syntax axioms themselves (and the $f's of course.)
e's and $d's associated with those $a statements, and any $f statements. And, for maximum speed of parsing, Syntax RPN "proofs" would be used instead of "ASCII shorthand", except on the syntax axioms themselves (and the $f's of course.)
Here is an example. Labels are integers assigned sequentially. Axiom ASCII shorthand formulas are used instead of RPN syntax "proofs" – for clarity of the demonstration:
$c ( ) -> wff |-
$v ph ps ch
1 $f wff ph $.
2 $f wff ps $.
3 $f wff ch $.
4 $a wff ( ph -> ps ) $.
5 $a |- ( ph -> ( ps -> ph ) ) $.
6 $a |- ( ( ph -> ( ps -> ch ) ) ->
( ( ph -> ps ) -> ( ph -> ch ) ) ) $.
${
7 $e |- ph $.
8 $e |- ( ph -> ps ) $.
9 $a |- ps $.
$}
${ $( corresponds to a1i = "ph ==> ( ps -> ph )" $)
10 $e $.
11 $p $= 10 5 9 $.
$}
${ $( corresponds to a2i = "( ph -> ( ps -> ch ) ) ==>
( ( ph -> ps ) -> ( ph -> ch ) )"
12 $e $.
13 $p $= 12 6 9 $.
$}
In fact, everything after the "$}" following statement 9 could be compressed down to a stream of integers: "10 11 10 5 9 12 13 12 6 9".
To recreate the formulas dynamically one would unify the input .mm $p statements in sequence as they are read in. (And we'd need a .mm file parser capable of handing this abbreviated format!)
P.S. Godelizing is then obvious: 2**10 * 3**11 * 5**10 … (De-godelizing is much harder, of course…)
What this idea is really saying, I believe, is that because of Metamath's regularity of structure, the most general form of a theorem is fully described by the tree/RPN-list of the theorems used in its derivation -- where "derivation" is used exchangeably with "proof". Everything else is technically redundant because it can be recomputed with known algorithms.
Additional comression of a .mm file is possible using this method with addition of a search for repeated sub-proofs as each theorem is being added to the end of the stream.
I don't know that this idea has any practical value, except as a method for obfuscating a Metamath file – but there are possiblities. For example, once everything extraneous is eliminated patterns and similarities between different systems might be elucidated (by someone with a huge, densely packed brain.) The important thing is the idea that this can be done in theory because the idea provides insight into the nature of a logical system in Metamath.
What you describe is similar to how proofs are stored in mm solitaire (with the obvious limitations of that applet). Off and on I have pondered eliminating the syntax steps as an alternate proof notation for Metamath. The main disadvantage is that we would lose the speed of proof verification - the syntax steps effectively have worked out the unifications in advance, that would have to be recomputed with a unification algorithm. Raph and I had a number of discussions about whether to include syntax steps in Ghilbert, and in the end he also opted to keep them for verification speed reasons. The verification speed of Metamath is an advantage over some other verifiers, taking seconds rather than minutes or hours. Or 500ms for the Ghilbert version of set.mm in Shullivan, which is almost certainly the speed record of any existing verifier for that large a body of math knowledge.
Like you, I find the idea of no syntax steps clean and philosophically appealing. And the idea that "the proof is the mathematics", so that stating the theorem itself becomes irrelevant, is embodied in how mm solitaire works - the user never specifies the theorem he/she wants; the theorem is whatever results from the proof.
Here are some statistics for today's set.mm: the size is 6.7MB with 9595 theorems. The compressed proofs represent 3.6MB of this. I did an experiment to strip out the syntax-building steps in set.mm, and we end up with 241K (non-compressed) logical steps for all proofs of all theorems. From here you can calculate the savings of your proposed notation. – [norm] 15 Mar 2008
—
OK, in my number stream format above,
"10 11 10 5 9 12 13 12 6 9"
Where 10 is the logical hypothesis for theorem 11
a) 10 is identified as a logical hypothesis by virtue of the fact that it is immediately followed by a number that is greater than 10 (because only backward references are permissible within a theorem);
b) the end of 11's proof is indicated by the number 12, which is the logical hypothesis for 13.
And because only backward references are allowed in the theorem number stream, it is possible to use variable length words to encode the numbers. The trick is to have a convention about when to change over to a one-bit longer word. That is as follows: Say we are encoding the first 7 statements, which can be done using 3 bit words. Then the first time the number 7 is encoded the following word is, by convention, a 4 bit word. Later, after 15 is first encoded we immediately switch to 5 bit words, and so on.
--ocat
Oops, I somehow read too fast and missed that, so I took out my irrelevant verbiage on how to "improve" your notation. – norm
Re: logical hypotheses: these references are local to a theorem, so the numbers 0 → 127 could be reserved for them and reused. The existence and number of them can be deduced from their usage in a theorem's proof. The maximum number seen in one theorem in set.mm, at last check, is 19 (BTW, mmj2 imposes an arbitrary constant maximum of 99 which would require a recompilation to modify.) Call the upper limit "H". Also, every logical axiom and definition must be assigned a number, which for simplicity would range from H + 1 to a maximum of say, H + 256, AKA "J" (depending on the .mm file to be compressed.) So numbering of theorems would begin at J + 1, or say, 384. Since there are way more than 128 logical hypotheses in set.mm this would result in significant savings in the output number stream.
Re: inferred theorem numbers, this is doable but still leaves the need for an end of proof "marker". The end of proof marker would need to be a unique bit pattern in the current VLW bit space, such as b'00000000000000'. However, the amount of savings would be infintesimal because if you're going to output a unique bit pattern why not just output the next theorem's number? So, I think, this idea's complexities don't pay off enough to justify its implementation. (Alternatively a proof length number could be encoded but any savings would be offset by the complications of imposing limits on proof lengths, etc.)
The only way to know the total resulting length with the VLW idea is to actually run the algorithm. That is because each proof has a different length, with the later proofs tending to be larger and also being located in the longer VLW area of the stream. But I think the average VLW word length would be 13 bits or so – assuming we have about 10K assertions, and 256K label numbers and proof steps, then the output would be about 416K bytes, not counting elimination of repeated subproofs and zipping.
P.S. This is not all purely theoretical. The mmj2 parallel/regression tests include runs to rederive distinct variable restrictions and proof step formulas (see RunParm? "ProofAsstBatchTest?" and keywords "DeriveFormulas?" and "UpdateDJs?"). The 'qed' and logical hypothesis formulas are not rederived, and of these two the only thing which I take on faith as a wondrous matter is that the hypotheses can be derived given the proof. So pretty much, this has all been done already and we know it works, but knowing that we can output set.mm and ql.mm as very short compressed bit streams is different than having the will to do so – for that a grant from a philanthropist would be required :-) --ocat
Proof Fragments
I'm trying to figure out how to implement a proof search using MapReduce? (or Hadoop). One problem is that unification of a derivation step formula's hypothesis with a particular assertion may impose constraints on a Work Variable in that step's formula and unification of another formula elsewhere in the proof, say in another hypothesis or proof step, may impose other constraints on the same Work Variable – these constraints must not be inconsistent. This is an issue for parallel processing searches and complicates things.
My big idea today is based on the work we've been talking about wherein everything that characterizes the most general form of a proof is contained in the tree/RPN-list of the proof step assertions and logical hypotheses (we don't need the syntax or variables.) So a search algorithm could return a "Proof Fragment" that consists of just a partial proof sub-tree, perhaps with "null" indicating missing sub-sub-trees. The proof fragment would thus, just be a not-inconsistent tree/RPN-list of assertions (labels) and logical hypotheses (labels), which fit together in a certain way which is not inconsistent. For example, "NULL a2i ax-mp" is a "proof fragment", and so is "a2i NULL ax-mp"; what purpose they serve in the final proof is unknown, we just know that they should be considered in the current context. (One reason why this is a "good" idea is that each process and context may have its own set of variables in play, and transmitting back variable-related information to the "Master" process is really a bogosity (with all the renames and lookups, etc.))
This idea is a little bit wacky, because obviously there are infinity+ proof fragments, but the parallel to DNA fragments is unavoidable, and we all know how that worked out :-)
--ocat 18-Mar-2008
Spin off Spin-off Idea: Reverse Metamath
New Idea which is a take-off on the idea above, "=Spin-off Idea: Maximal Compression of a .mm File=".
The idea is that maximally compressing a Metamath file reduces it to its most pure informational content – or, to the highest signal to noise ratio. Minimal entropy.
We then wonder, what if the axioms were excluded from the compressed file? Then, only the proof numbers would remain, and certain questions would arise:
1) Is it possible for two valid different Sans-axiom-Maximally-Compressed Metamath files to describe different mathematical systems – i.e. with different meanings?
2) Could we infer the axioms from the proof numbers alone -- and what would be the smallest set of proofs which would completely eliminate the unknowns?
Just as an example, assume we have the proof "ax-1 ax-mp ax-mp", which asserts the theorem that hypothesis reiteration is justified (e.g. ph |- ph ).
What can we deduce?
Answer:
1) That ax-mp has at least one logical hypothesis, assuming that a theorem's 'qed' step justification theorem (the Ref) will always have a logical hypothesis (otherwise the theorem would be just a substitution instance of another theorem -- except perhaps, with different $d restrictions.)
2) And ???
Reverse engineering the Logical Axioms for a .mm file using just the Maximally Compressed bitstream (see MaximallyCompressedMetamathDatabases is an extremely difficult problem, if not impossible – because the $d restrictions are not present in the Maximally Compressed bitstream and are rederived from the axioms.
Also, we do not know anything about the Meta-content of the file – for example, are they using "|-" or are there (even) multiple types of logical statements (E.G. perhaps they use "It is not provable that…" as well as "It is provably true that …" and "It is provably false that…").
Perhaps the inventors of the input bitstream are using 3-valued logic. Perhaps they employ a deliberately ambiguous grammar.
Very challenging!
What is kind of interesting is that to "solve" the problem one can begin with "|- &W1" for the first axiom, "|- &W2" for the 2nd, etc., and then gradually infer structure without actually knowing the connectives – that is, the connectives would need to be represented by their own variables. Solving the problem would mean scanning the input and showing that the proposed solution is not demonstrably inconsistent…and then plugging in a model language which is consistent with what has been inferred so far…knowing that if the bitstream were extended that new data might introduce inconsistencies in what had been inferred up to that point.