Description: The Axiom of Separation
of IZF set theory. Axiom 6 of [Crosilla], p.
"Axioms of CZF and IZF" (with unnecessary quantifier removed,
and with a
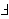   condition replaced by a distinct
variable constraint between condition replaced by a distinct
variable constraint between
 and and  ). ).
The Separation Scheme is a weak form of Frege's Axiom of Comprehension,
conditioning it (with    ) so that it asserts the
existence of a
collection only if it is smaller than some other collection ) so that it asserts the
existence of a
collection only if it is smaller than some other collection  that
already exists. This prevents Russell's paradox ru 2908. In
some texts,
this scheme is called "Aussonderung" or the Subset Axiom. that
already exists. This prevents Russell's paradox ru 2908. In
some texts,
this scheme is called "Aussonderung" or the Subset Axiom.
(Contributed by NM, 11-Sep-2006.) |