Description: Axiom of Left Equality
for Binary Predicate. One of the equality and
substitution axioms for a non-logical predicate in our predicate calculus
with equality. It substitutes equal variables into the left-hand side of
an arbitrary binary predicate 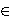 , which we will use for the set
membership relation when set theory is introduced. This axiom scheme is a
sub-scheme of Axiom Scheme B8 of system S2 of [Tarski], p. 75, whose
general form cannot be represented with our notation. Also appears as
Axiom scheme C12' in [Megill] p. 448 (p. 16
of the preprint).
"Non-logical" means that the predicate is not a primitive of
predicate
calculus proper but instead is an extension to it. "Binary"
means that
the predicate has two arguments. In a system of predicate calculus with
equality, like ours, equality is not usually considered to be a
non-logical predicate. In systems of predicate calculus without equality,
it typically would be. (Contributed by NM,
5-Aug-1993.) |
