Theorem weq 1643

Description: Extend wff definition to include atomic formulas using the equality predicate.

(Instead of introducing weq 1643 as an axiomatic statement, as was done in an older version of this database, we introduce it by "proving" a special case of set theory's more general wceq 1642. This lets us avoid overloading the 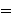= connective, thus preventing ambiguity that would complicate certain Metamath parsers. However, logically weq 1643 is considered to be a primitive syntax, even though here it is artificially "derived" from wceq 1642. Note: To see the proof steps of this syntax proof, type "show proof weq /all" in the Metamath program.) (Contributed by NM, 24-Jan-2006.)

Assertion

Ref	Expression
weq	wff x = y

Proof of Theorem weq

Step	Hyp	Ref	Expression
1		wceq 1642	1 wff x = y

Syntax hints:   = wceq 1642

This theorem is referenced by:  equs3  1644  speimfw  1645  spimfw  1646  ax11i  1647  sbequ2  1650  sb1  1651  sbimi  1652  a9ev  1656  exiftru  1657  exiftruOLD  1658  spimeh  1667  spimw  1668  spnfw  1670  equid  1676  equidOLD  1677  nfequid  1678  equcomi  1679  equcom  1680  equcoms  1681  equtr  1682  equtrr  1683  equequ1  1684  equequ1OLD  1685  equequ2  1686  stdpc6  1687  equtr2  1688  ax12b  1689  ax12bOLD  1690  spfw  1691  spnfwOLD  1692  spw  1694  spvwOLD  1695  spfalwOLD  1699  19.2OLD  1700  cbvalw  1701  cbvalvw  1702  cbvexvw  1703  alcomiw  1704  hba1w  1707  hbe1w  1708  elequ1  1713  elequ2  1715  ax9dgen  1716  ax11w  1721  ax11dgen  1722  ax11wdemo  1723  ax12w  1724  ax12dgen1  1725  ax12dgen2  1726  ax12dgen3  1727  sp  1747  spOLD  1748  spimehOLD  1821  equsalhw  1838  equsalhwOLD  1839  dvelimhw  1849  cbv3hv  1850  cbv3hvOLD  1851  equs5a  1887  equs5e  1888  sbequ1  1918  sbequ12  1919  sbequ12r  1920  sbequ12a  1921  sbid  1922  sb4a  1923  sb4e  1924  ax12olem1  1927  ax12olem2  1928  ax12olem3  1929  ax12olem4  1930  ax12olem5  1931  ax12olem6  1932  ax12  1935  ax10lem1  1936  ax10lem2  1937  ax10lem3  1938  dvelimv  1939  dveeq2  1940  ax10lem4  1941  ax10lem5  1942  ax10lem6  1943  ax10  1944  a16g  1945  aecoms  1947  naecoms  1948  ax9  1949  ax9o  1950  a9e  1951  ax10o  1952  hbae  1953  nfae  1954  hbnae  1955  nfnae  1956  hbnaes  1957  nfeqf  1958  equs4  1959  equsal  1960  equsex  1962  dvelimh  1964  dral1  1965  dral2  1966  drex1  1967  drex2  1968  drnf1  1969  drnf2  1970  exdistrf  1971  nfald2  1972  nfexd2  1973  spimt  1974  spim  1975  spime  1976  spimed  1977  cbv1h  1978  cbv2h  1980  cbv3  1982  cbv3h  1983  cbval  1984  cbvex  1985  chvar  1986  equvini  1987  equveli  1988  equs45f  1989  aev  1991  ax11v2  1992  ax11a2  1993  ax11b  1995  equs5  1996  dvelimf  1997  spv  1998  speiv  2000  equvin  2001  cbval2  2004  cbvex2  2005  cbvexd  2009  cbvaldva  2010  cbvexdva  2011  cbvex4v  2012  cleljust  2014  cleljustALT  2015  dveeq1  2018  ax15  2021  drsb1  2022  sb2  2023  stdpc4  2024  sbft  2025  sb6x  2029  sbequ5  2031  sbequ6  2032  equsb1  2034  equsb2  2035  sbied  2036  sbiedv  2037  sbie  2038  sb6f  2039  sb5f  2040  hbsb2a  2041  hbsb2e  2042  ax16i  2046  ax16ALT2  2048  a16gALT  2049  a16gb  2050  a16nf  2051  sb3  2052  sb4  2053  sb4b  2054  dfsb2  2055  dfsb3  2056  hbsb2  2057  nfsb2  2058  sbequi  2059  sbequ  2060  drsb2  2061  sbn  2062  sbi1  2063  sbequ8  2079  nfsb4t  2080  nfsb4  2081  dvelimdf  2082  sbco  2083  sbidm  2085  sbco2  2086  sbco3  2088  sbcom  2089  sb5rf  2090  sb6rf  2091  sb9i  2094  ax11v  2096  sb56  2098  sb6  2099  sb5  2100  equsb3lem  2101  equsb3  2102  hbs1  2105  nfsb  2109  nfsbd  2111  2sb5  2112  2sb6  2113  sbcom2  2114  pm11.07  2115  sb6a  2116  2sb5rf  2117  2sb6rf  2118  dfsb7  2119  sb7f  2120  sb10f  2122  sbelx  2124  sbel2x  2125  sbal1  2126  sbal  2127  exsb  2130  2exsb  2132  dvelimALT  2133  sbal2  2134  ax9from9o  2148  aecom-o  2151  aecoms-o  2152  hbae-o  2153  dral1-o  2154  ax11  2155  ax12from12o  2156  equid1  2158  hbequid  2160  nfequid-o  2161  equidqe  2173  ax4sp1  2174  equidq  2175  equid1ALT  2176  ax10from10o  2177  naecoms-o  2178  hbnae-o  2179  dvelimf-o  2180  dral2-o  2181  aev-o  2182  ax17eq  2183  dveeq2-o  2184  dveeq2-o16  2185  a16g-o  2186  dveeq1-o  2187  dveeq1-o16  2188  ax17el  2189  ax10-16  2190  ax11f  2192  ax11eq  2193  ax11el  2194  ax11indn  2195  ax11indi  2196  ax11indalem  2197  ax11inda2ALT  2198  ax11inda2  2199  ax11inda  2200  ax11v2-o  2201  ax11a2-o  2202  ax10o-o  2203  eujustALT  2207  eumo0  2228  eu2  2229  eu3  2230  mo2  2233  mo3  2235  mo4f  2236  eu4  2243  moanim  2260  2eu5  2288  euequ1  2292  axi11e  2332  cleqh  2450  abbib  2464  nfrmod  2785  nfrmo  2787  cbvraldva2  2840  cbvrexdva2  2841  cbvraldva  2842  cbvrexdva  2843  cbvrex2v  2845  sbralie  2849  rmo4  3030  reu4  3031  2reu5lem3  3044  2reu5  3045  sbsbc  3051  sbc8g  3054  sbc2or  3055  sbcco2  3070  sbc5  3071  sbcralt  3119  sbcralg  3121  sbcrexg  3122  sbcreug  3123  rmo2  3132  rmo2i  3133  rmo3  3134  sbcel12g  3152  sbceqg  3153  cbvralcsf  3199  cbvrabcsf  3202  ninjust  3211  csbifg  3691  axxpprim  4091  axcnvprim  4092  axssetprim  4093  axsiprim  4094  axtyplowerprim  4095  axins2prim  4096  axins3prim  4097  snex  4112  pwadjoin  4120  preqr2g  4127  preq12bg  4129  1cex  4143  opkabssvvk  4209  sikss1c1c  4268  opkelidkg  4275  idkssvvk  4282  dfpw12  4302  dfidk2  4314  unipw1  4326  eqpw1uni  4331  dfeu2  4334  dfiota2  4341  sb8iota  4347  uniabio  4350  iotanul  4355  iota4  4358  csbiotag  4372  peano2  4404  addcid1  4406  nnc0suc  4413  nncaddccl  4420  nnsucelrlem1  4425  nnsucelr  4429  nndisjeq  4430  preaddccan2  4456  ltfintrilem1  4466  ltfintri  4467  ssfin  4471  vfinnc  4472  ncfinraise  4482  ncfinlower  4484  nnpw1ex  4485  eqtfinrelk  4487  oddfinex  4505  evenoddnnnul  4515  evenodddisjlem1  4516  evenodddisj  4517  nnadjoinlem1  4520  nnadjoin  4521  nnadjoinpw  4522  nnpweq  4524  sfindbl  4531  sfintfin  4533  tfinnn  4535  spfinsfincl  4540  vfinspsslem1  4551  vfinspss  4552  vfinspclt  4553  dfphi2  4570  phi11lem1  4596  proj1op  4601  proj2op  4602  copsexg  4608  phidisjnn  4616  phialllem1  4617  opeq  4620  cbvopab  4631  sbcbrg  4686  opelopabsb  4698  br1stg  4731  dfima2  4746  dfco1  4749  dfsi2  4752  opeliunxp  4821  ralxpf  4828  opabid2  4862  ideqg  4869  ideqg2  4870  dfdmf  4906  dmi  4920  iss  5001  dfres2  5003  opabresid  5004  intasym  5029  intirr  5030  dmsnopg  5067  coi1  5095  dfxp2  5114  dffun2  5120  dffun3  5121  dffun4  5122  dffun5  5123  dffun6f  5124  nfunv  5139  funun  5147  fun11  5160  fununi  5161  fun11iun  5306  fv2  5325  elfv  5327  tz6.12-2  5347  dffn5  5364  fnasrn  5418  fvi  5443  dff13  5472  isotr  5496  dfid4  5504  1stfo  5506  2ndfo  5507  swapf1o  5512  fununiq  5518  funsi  5521  oprabid  5551  cbvoprab12  5570  oprabid2  5647  mptresid  5721  trtxp  5782  brtxp  5784  elfix  5788  oqelins4  5795  fntxp  5805  addcfnex  5825  funsex  5829  qrpprod  5837  dmpprod  5841  fnpprod  5844  pw1fnf1o  5856  fnfullfunlem1  5857  fnfullfunlem2  5858  fvfullfunlem1  5862  fvfullfunlem2  5863  fvfullfunlem3  5864  clos1basesuc  5883  antisymex  5913  foundex  5915  extex  5916  frd  5923  extd  5924  antird  5929  antid  5930  frds  5936  weds  5939  po0  5940  ider  5944  ssetpov  5945  idssen  6041  fundmen  6044  xpassen  6058  enpw1lem1  6062  enpw1  6063  enmap2lem4  6067  enmap1lem4  6073  enprmaplem3  6079  enprmaplem5  6081  enprmaplem6  6082  nenpw1pwlem2  6086  mucex  6134  ncspw1eu  6160  ceex  6175  ce0addcnnul  6180  ce0nn  6181  el2c  6192  lecponc  6214  leconnnc  6219  dflec3  6222  tcfnex  6245  nclenn  6250  csucex  6260  nnltp1c  6263  addccan2nclem1  6264  addccan2nc  6266  nmembers1lem1  6269  nmembers1lem3  6271  nmembers1  6272  nncdiv3  6278  nnc3n3p1  6279  spacind  6288  nchoicelem3  6292  nchoicelem12  6301  nchoicelem17  6306  nchoicelem19  6308  fnfreclem1  6318  fnfrec  6321  scancan  6332