Description: If  is a wff, so is is a wff, so is 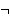  or "not or "not  ." Part of the
recursive definition of a wff (well-formed formula). In classical logic
(which is our logic), a wff is interpreted as either true or false. So if ." Part of the
recursive definition of a wff (well-formed formula). In classical logic
(which is our logic), a wff is interpreted as either true or false. So if
 is true,
then is true,
then 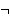  is false; if is false; if  is false, then is false, then
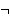  is true.
Traditionally, Greek letters are used to represent
wffs, and we follow this convention. In propositional calculus, we define
only wffs built up from other wffs, i.e. there is no starting or
"atomic"
wff. Later, in predicate calculus, we will extend the basic wff
definition by including atomic wffs (weq 1643 and wel 1711). is true.
Traditionally, Greek letters are used to represent
wffs, and we follow this convention. In propositional calculus, we define
only wffs built up from other wffs, i.e. there is no starting or
"atomic"
wff. Later, in predicate calculus, we will extend the basic wff
definition by including atomic wffs (weq 1643 and wel 1711). |