Description: Axiom ax-11o 1811 ("o" for "old") was the
original version of ax-11 1494,
before it was discovered (in Jan. 2007) that the shorter ax-11 1494 could
replace it. It appears as Axiom scheme C15' in [Megill] p. 448 (p. 16 of
the preprint). It is based on Lemma 16 of [Tarski] p. 70 and Axiom C8 of
[Monk2] p. 105, from which it can be proved
by cases. To understand this
theorem more easily, think of " 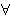     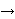..." as informally
meaning "if
and are distinct
variables, then..." The
antecedent becomes false if the same variable is substituted for and
, ensuring the
theorem is sound whenever this is the case. In some
later theorems, we call an antecedent of the form 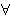a
"distinctor."
This axiom is redundant, as shown by Theorem ax11o 1810.
This axiom is obsolete and should no longer be used. It is proved above
as Theorem ax11o 1810. (Contributed by NM, 5-Aug-1993.)
(New usage is discouraged.) |
