Description: Define a recursive
definition generator on 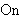 (the class of ordinal
numbers) with characteristic function (the class of ordinal
numbers) with characteristic function  and initial value and initial value 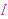 .
This rather amazing operation allows us to define, with compact direct
definitions, functions that are usually defined in textbooks only with
indirect self-referencing recursive definitions. A recursive definition
requires advanced metalogic to justify - in particular, eliminating a
recursive definition is very difficult and often not even shown in
textbooks. On the other hand, the elimination of a direct definition is
a matter of simple mechanical substitution. The price paid is the
daunting complexity of our .
This rather amazing operation allows us to define, with compact direct
definitions, functions that are usually defined in textbooks only with
indirect self-referencing recursive definitions. A recursive definition
requires advanced metalogic to justify - in particular, eliminating a
recursive definition is very difficult and often not even shown in
textbooks. On the other hand, the elimination of a direct definition is
a matter of simple mechanical substitution. The price paid is the
daunting complexity of our 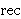 operation (especially when df-recs 6202
that it is built on is also eliminated). But once we get past this
hurdle, definitions that would otherwise be recursive become relatively
simple. In classical logic it would be easier to divide this definition
into cases based on whether the domain of operation (especially when df-recs 6202
that it is built on is also eliminated). But once we get past this
hurdle, definitions that would otherwise be recursive become relatively
simple. In classical logic it would be easier to divide this definition
into cases based on whether the domain of  is zero, a successor, or
a limit ordinal. Cases do not (in general) work that way in
intuitionistic logic, so instead we choose a definition which takes the
union of all the results of the characteristic function for ordinals in
the domain of is zero, a successor, or
a limit ordinal. Cases do not (in general) work that way in
intuitionistic logic, so instead we choose a definition which takes the
union of all the results of the characteristic function for ordinals in
the domain of  .
This means that this definition has the expected
properties for increasing and continuous ordinal functions, which
include ordinal addition and multiplication. .
This means that this definition has the expected
properties for increasing and continuous ordinal functions, which
include ordinal addition and multiplication.
For finite recursion we also define df-frec 6288 and for suitable
characteristic functions df-frec 6288 yields the same result as 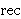 restricted to
restricted to 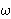 , as seen at frecrdg 6305. , as seen at frecrdg 6305.
Note: We introduce 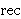 with the philosophical goal of being
able to eliminate all definitions with direct mechanical
substitution
and to verify easily the soundness of definitions. Metamath
itself
has no built-in technical limitation that prevents multiple-part
recursive definitions in the traditional textbook style.
(Contributed
by Jim Kingdon, 19-May-2019.) with the philosophical goal of being
able to eliminate all definitions with direct mechanical
substitution
and to verify easily the soundness of definitions. Metamath
itself
has no built-in technical limitation that prevents multiple-part
recursive definitions in the traditional textbook style.
(Contributed
by Jim Kingdon, 19-May-2019.) |