Description: Define the 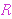 -coset of -coset of  . Exercise 35 of [Enderton] p. 61. This
is called the equivalence class of . Exercise 35 of [Enderton] p. 61. This
is called the equivalence class of  modulo modulo 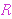 when when 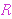 is
an
equivalence relation. In this case, is
an
equivalence relation. In this case,  is a representative (member) of
the equivalence class is a representative (member) of
the equivalence class 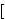  ![]](rbrack.gif) 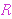 , which contains all sets that are
equivalent to , which contains all sets that are
equivalent to  .
Definition of [Enderton] p. 57 uses the
notation .
Definition of [Enderton] p. 57 uses the
notation
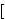  ![]](rbrack.gif) (subscript) (subscript) 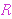 , although we simply follow the brackets by , although we simply follow the brackets by
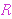 since we don't
have subscripted expressions. For an alternate
definition, see dfec2 5949. (Contributed by set.mm contributors,
22-Feb-2015.) since we don't
have subscripted expressions. For an alternate
definition, see dfec2 5949. (Contributed by set.mm contributors,
22-Feb-2015.) |