| Description: Extend wff definition to
include class equality.
For a general discussion of the theory of classes, see
https://us.metamath.org/mpeuni/mmset.html#class.
(The purpose of introducing 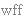  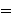 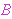 here, and not in set
theory
where it belongs, is to allow us to express i.e. "prove" the
weq 1643
of
predicate calculus in terms of the wceq 1642
of set theory, so that we
don't "overload" the here, and not in set
theory
where it belongs, is to allow us to express i.e. "prove" the
weq 1643
of
predicate calculus in terms of the wceq 1642
of set theory, so that we
don't "overload" the 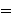 connective with two syntax definitions. This
is done to prevent ambiguity that would complicate some Metamath
parsers. For example, some parsers - although not the Metamath program
- stumble on the fact that the connective with two syntax definitions. This
is done to prevent ambiguity that would complicate some Metamath
parsers. For example, some parsers - although not the Metamath program
- stumble on the fact that the 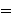 in in  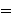  could be the could be the 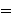 of
either weq 1643 or wceq 1642, although mathematically it makes no
difference.
The class variables of
either weq 1643 or wceq 1642, although mathematically it makes no
difference.
The class variables  and and 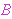 are
introduced temporarily for the
purpose of this definition but otherwise not used in predicate calculus.
See df-cleq 2346 for more information on the set theory usage
of
wceq 1642.) are
introduced temporarily for the
purpose of this definition but otherwise not used in predicate calculus.
See df-cleq 2346 for more information on the set theory usage
of
wceq 1642.) |