| Description: Define the class of
natural numbers as the smallest inductive set, which
is valid provided we assume the Axiom of Infinity. Definition 6.3 of
[Eisenberg] p. 82.
Note: the natural numbers 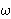 are a subset of the ordinal numbers
df-on 4433. Later, when we define complex numbers, we
will be able to
also define a subset of the complex numbers (df-inn 9072) with analogous
properties and operations, but they will be different sets. are a subset of the ordinal numbers
df-on 4433. Later, when we define complex numbers, we
will be able to
also define a subset of the complex numbers (df-inn 9072) with analogous
properties and operations, but they will be different sets.
We are unable to use the terms finite ordinal and natural number
interchangeably, as shown at exmidonfin 7333. (Contributed by NM,
6-Aug-1994.) Use its alias dfom3 4658 instead for naming consistency with
set.mm. (New usage is discouraged.) |