Description: Axiom of bundling. The
general idea of this axiom is that two variables
are either distinct or non-distinct. That idea could be expressed as
   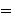 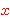 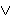     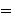 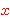 . However, we instead choose an axiom
which has many of the same consequences, but which is different with
respect to a universe which contains only one object. . However, we instead choose an axiom
which has many of the same consequences, but which is different with
respect to a universe which contains only one object.    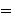 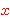 holds
if holds
if  and and 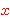 are the same variable,
likewise for are the same variable,
likewise for  and and  ,
and ,
and  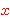   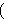 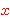   
  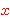 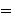  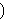 holds if holds if  is distinct from
the others (and the universe has at least two objects). is distinct from
the others (and the universe has at least two objects).
As with other statements of the form "x is decidable (either true or
false)", this does not entail the full Law of the Excluded Middle
(which
is the proposition that all statements are decidable), but instead merely
the assertion that particular kinds of statements are decidable (or in
this case, an assertion similar to decidability).
This axiom implies ax-i12 1485 as can be seen at axi12 1494. Whether ax-bndl 1486
can be proved from the remaining axioms including ax-i12 1485 is not known.
The reason we call this "bundling" is that a statement without a
distinct
variable constraint "bundles" together two statements, one in
which the
two variables are the same and one in which they are different.
(Contributed by Mario Carneiro and Jim Kingdon,
14-Mar-2018.) |