Description: Define plus infinity.
Note that the definition is arbitrary, requiring
only that 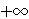 be a set not in
be a set not in 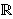 and
different from and
different from 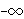 (df-mnf 8145). We use
(df-mnf 8145). We use 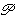  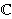 to
make it independent of the
construction of to
make it independent of the
construction of 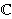 , and Cantor's Theorem will show that it is
different from any member of , and Cantor's Theorem will show that it is
different from any member of 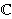 and therefore and therefore 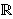 . See pnfnre 8149
and mnfnre 8150, and we'll also be able to prove . See pnfnre 8149
and mnfnre 8150, and we'll also be able to prove 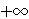 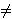 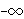 . .
A simpler possibility is to define 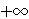 as as 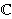 and and 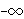 as
as
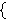 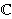 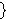 , but that approach requires the Axiom of
Regularity to show
that , but that approach requires the Axiom of
Regularity to show
that 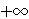 and and
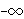 are different
from each other and from all
members of are different
from each other and from all
members of 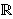 .
(Contributed by NM, 13-Oct-2005.)
(New usage is discouraged.) .
(Contributed by NM, 13-Oct-2005.)
(New usage is discouraged.) |