| Description: Define the multiplicative
identity, i.e., the monoid identity (df-0g 13205)
of the multiplicative monoid (df-mgp 13798) of a ring-like structure. This
multiplicative identity is also called "ring unity" or
"unity element".
This definition works by transferring the multiplicative operation from
the 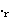 slot to
the slot to
the 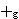 slot and
then looking at the element which
is then the slot and
then looking at the element which
is then the 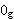 element, that is an identity with respect to the
operation which started out in the
element, that is an identity with respect to the
operation which started out in the 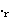 slot. slot.
See also dfur2g 13839, which derives the "traditional"
definition as the
unique element of a ring which is left- and right-neutral under
multiplication. (Contributed by NM, 27-Aug-2011.) (Revised by Mario
Carneiro, 27-Dec-2014.) |