Description: Double negation of
stability of a formula. Intuitionistic logic refutes
unstability (but does not prove stability) of any formula. This theorem
can also be proved in classical refutability calculus (see
https://us.metamath.org/mpeuni/bj-peircestab.html) but not in minimal
calculus (see https://us.metamath.org/mpeuni/bj-stabpeirce.html). See
nnnotnotr 16125 for the version not using the definition of
stability.
(Contributed by BJ, 9-Oct-2019.) Prove it in  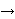    -intuitionistic calculus with definitions (uses of ax-ia1 106, ax-ia2 107,
ax-ia3 108 are via sylibr 134, necessary for definition unpackaging), and in
-intuitionistic calculus with definitions (uses of ax-ia1 106, ax-ia2 107,
ax-ia3 108 are via sylibr 134, necessary for definition unpackaging), and in
 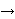  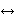    -intuitionistic calculus, following a discussion
with Jim Kingdon. (Revised by BJ,
27-Oct-2024.) -intuitionistic calculus, following a discussion
with Jim Kingdon. (Revised by BJ,
27-Oct-2024.) |