Description: Define class of all
groups. A group is a monoid (df-mnd 13364) whose
internal operation is such that every element admits a left inverse
(which can be proven to be a two-sided inverse). Thus, a group  is
an algebraic structure formed from a base set of elements (notated is
an algebraic structure formed from a base set of elements (notated
 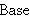    per df-base 12953) and an internal group operation
(notated per df-base 12953) and an internal group operation
(notated  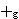    per df-plusg 13037). The operation combines any
two elements of the group base set and must satisfy the 4 group axioms:
closure (the result of the group operation must always be a member of
the base set, see grpcl 13455), associativity (so per df-plusg 13037). The operation combines any
two elements of the group base set and must satisfy the 4 group axioms:
closure (the result of the group operation must always be a member of
the base set, see grpcl 13455), associativity (so
   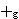
  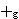      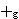   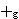    for any a, b, c, see
grpass 13456), identity (there must be an element for any a, b, c, see
grpass 13456), identity (there must be an element 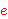   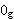    such
that such
that 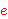 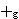    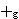 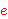   for
any a), and inverse (for each element a
in the base set, there must be an element for
any a), and inverse (for each element a
in the base set, there must be an element   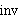   in the base set
such that in the base set
such that  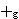    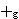   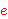 ).
It can be proven that the identity
element is unique (grpideu 13458). Groups need not be commutative; a
commutative group is an Abelian group. Subgroups can often be formed
from groups. An example of an (Abelian) group is the set of complex
numbers ).
It can be proven that the identity
element is unique (grpideu 13458). Groups need not be commutative; a
commutative group is an Abelian group. Subgroups can often be formed
from groups. An example of an (Abelian) group is the set of complex
numbers 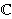 over
the group operation over
the group operation 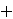 (addition). Other
structures include groups, including unital rings and fields.
(Contributed by NM, 17-Oct-2012.) (Revised by Mario Carneiro,
6-Jan-2015.)
(addition). Other
structures include groups, including unital rings and fields.
(Contributed by NM, 17-Oct-2012.) (Revised by Mario Carneiro,
6-Jan-2015.) |