| Description: Define a subring of a
ring as a set of elements that is a ring in its
own right and contains the multiplicative identity.
The additional constraint is necessary because the multiplicative
identity of a ring, unlike the additive identity of a ring/group or the
multiplicative identity of a field, cannot be identified by a local
property. Thus, it is possible for a subset of a ring to be a ring
while not containing the true identity if it contains a false identity.
For instance, the subset  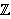 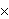 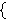 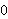 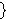  of of  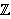 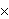 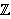  (where
multiplication is componentwise) contains the false identity (where
multiplication is componentwise) contains the false identity
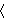 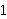  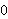 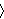 which preserves every element of the subset and thus
appears to be the identity of the subset, but is not the identity of the
larger ring. (Contributed by Stefan O'Rear,
27-Nov-2014.)
which preserves every element of the subset and thus
appears to be the identity of the subset, but is not the identity of the
larger ring. (Contributed by Stefan O'Rear,
27-Nov-2014.) |