Description: Define the class of all
undirected multigraphs. An (undirected)
multigraph consists of a set 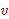 (of "vertices") and a function (of "vertices") and a function 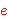 (representing indexed "edges") into subsets of
(representing indexed "edges") into subsets of 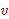 of cardinality two,
representing the two vertices incident to the edge. In contrast to a
pseudograph, a multigraph has no loop. This is according to Chartrand,
Gary and Zhang, Ping (2012): "A First Course in Graph
Theory.", Dover,
ISBN 978-0-486-48368-9, section 1.4, p. 26: "A multigraph M
consists of
a finite nonempty set V of vertices and a set E of edges, where every
two vertices of M are joined by a finite number of edges (possibly
zero). If two or more edges join the same pair of (distinct) vertices,
then these edges are called parallel edges." (Contributed by AV,
24-Nov-2020.) (Revised by Jim Kingdon,
3-Jan-2026.) of cardinality two,
representing the two vertices incident to the edge. In contrast to a
pseudograph, a multigraph has no loop. This is according to Chartrand,
Gary and Zhang, Ping (2012): "A First Course in Graph
Theory.", Dover,
ISBN 978-0-486-48368-9, section 1.4, p. 26: "A multigraph M
consists of
a finite nonempty set V of vertices and a set E of edges, where every
two vertices of M are joined by a finite number of edges (possibly
zero). If two or more edges join the same pair of (distinct) vertices,
then these edges are called parallel edges." (Contributed by AV,
24-Nov-2020.) (Revised by Jim Kingdon,
3-Jan-2026.) |