Description: Weak deduction theorem
that eliminates a hypothesis  , making it
become an antecedent. We assume that a proof exists for , making it
become an antecedent. We assume that a proof exists for  when the
class variable when the
class variable  is replaced with a specific class is replaced with a specific class 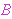 . The
hypothesis . The
hypothesis  should be assigned to the inference, and the
inference's hypothesis eliminated with elimhyp 3711. If the inference has
other hypotheses with class variable
should be assigned to the inference, and the
inference's hypothesis eliminated with elimhyp 3711. If the inference has
other hypotheses with class variable  , these can be kept by
assigning keephyp 3717 to them. For more information, see the
Deduction
Theorem https://us.metamath.org/mpeuni/mmdeduction.html 3717.
(Contributed by NM, 15-May-1999.) , these can be kept by
assigning keephyp 3717 to them. For more information, see the
Deduction
Theorem https://us.metamath.org/mpeuni/mmdeduction.html 3717.
(Contributed by NM, 15-May-1999.) |