Axiom ax-mp 5

Description: Rule of Modus Ponens. The postulated inference rule of propositional calculus. See e.g. Rule 1 of [Hamilton] p. 73. The rule says, "if ph is true, and ph implies ps, then ps must also be true". This rule is sometimes called "detachment", since it detaches the minor premise from the major premise. "Modus ponens" is short for "modus ponendo ponens", a Latin phrase that means "the mode that by affirming affirms" - remark in [Sanford] p. 39. This rule is similar to the rule of modus tollens mto 167.

Note: In some web page displays such as the Statement List, the symbols "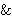& " and "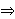=> " informally indicate the relationship between the hypotheses and the assertion (conclusion), abbreviating the English words "and" and "implies". They are not part of the formal language. (Contributed by NM, 30-Sep-1992.)

Hypotheses

Ref	Expression
min	|- ph
maj	|- (ph -> ps)

Assertion

Ref	Expression
ax-mp	|- ps

Detailed syntax breakdown of Axiom ax-mp

Step	Hyp	Ref	Expression
1		wps	1 wff ps

This axiom is referenced by:  mp2b  9  a1i  10  mp1i  11  a2i  12  mpd  14  mp2  17  idALT  20  notnotri  106  notnoti  115  pm2.24ii  124  mt4  129  pm2.61i  156  bi1  178  bi3  179  dfbi1  184  dfbi1gb  185  biimpi  186  bicomi  193  mpbi  199  mpbir  200  imbi1i  315  a1bi  327  tbt  333  nbn  336  biorfi  396  simpli  444  simpri  448  biantru  491  biantrur  492  mp2an  653  simp1i  964  simp2i  965  simp3i  966  3mix1i  1127  3mix2i  1128  3mix3i  1129  3jaoi  1245  nanbi1i  1298  nanbi2i  1299  trud  1323  merlem1  1407  merlem2  1408  merlem3  1409  merlem4  1410  merlem5  1411  merlem6  1412  merlem7  1413  merlem8  1414  merlem9  1415  merlem10  1416  merlem11  1417  merlem12  1418  merlem13  1419  luk-1  1420  luk-2  1421  luk-3  1422  luklem1  1423  luklem2  1424  luklem4  1426  luklem6  1428  luklem7  1429  luklem8  1430  ax2  1432  nic-mp  1436  nic-mpALT  1437  tbwsyl  1469  tbwlem2  1471  tbwlem3  1472  tbwlem4  1473  tbwlem5  1474  re1luk2  1476  re1luk3  1477  merco1lem1  1479  retbwax4  1480  retbwax2  1481  merco1lem2  1482  merco1lem3  1483  merco1lem4  1484  merco1lem5  1485  merco1lem6  1486  merco1lem7  1487  retbwax3  1488  merco1lem8  1489  merco1lem9  1490  merco1lem10  1491  merco1lem11  1492  merco1lem12  1493  merco1lem13  1494  merco1lem14  1495  merco1lem15  1496  merco1lem16  1497  merco1lem17  1498  merco1lem18  1499  retbwax1  1500  mercolem1  1502  mercolem2  1503  mercolem3  1504  mercolem4  1505  mercolem5  1506  mercolem6  1507  mercolem7  1508  mercolem8  1509  re1tbw1  1510  re1tbw2  1511  re1tbw3  1512  re1tbw4  1513  anmp  1516  mpto1  1533  mtp-or  1538  mtp-orOLD  1539  mpg  1548  exiftru  1657  spimeh  1667  spimw  1668  19.2OLD  1700  sp  1747  spi  1753  nfri  1762  19.9h  1780  19.9OLD  1784  19.21  1796  19.23  1801  spimehOLD  1821  cbv3hv  1850  exan  1882  sbid  1922  equvini  1987  speiv  2000  sbf  2026  sbco  2083  sbidm  2085  ax11vALT  2097  ax10-16  2190  eumoi  2245  moani  2256  darii  2303  barbari  2305  festino  2309  baroco  2310  cesaro  2311  camestros  2312  datisi  2313  disamis  2314  felapton  2317  darapti  2318  dimatis  2320  fresison  2321  calemos  2322  fesapo  2323  bamalip  2324  eqeq1i  2360  eqeq2i  2363  eleq1i  2416  eleq2i  2417  nfcrii  2483  neeq1i  2527  neeq2i  2528  necon3i  2556  rspec  2679  mprg  2684  r19.21  2701  r19.23  2730  raleqi  2812  rexeqi  2813  elexi  2869  ceqsal  2885  vtoclf  2909  vtoclef  2928  vtocle  2929  spcv  2946  spcev  2947  clel3  2978  elabf  2985  elab2  2989  elab3  2993  euxfr  3023  reueq  3034  rmoimi2  3038  sbsbc  3051  sbc8g  3054  sbc6  3073  sbcie  3081  csbvarg  3164  csbief  3178  csbie2  3182  sbnfc2  3197  elnin  3225  elcompl  3226  nineq1i  3238  nineq2i  3239  compleqi  3245  symdifeq1i  3252  symdifeq2i  3253  sseli  3270  sselii  3271  sseq1i  3296  sseq2i  3297  psseq1i  3359  psseq2i  3360  difeq1i  3382  difeq2i  3383  uneq1i  3415  uneq2i  3416  ineq1i  3454  ineq2i  3455  ssinss1  3484  necompl  3545  vn0  3558  abf  3585  disj2  3599  0dif  3622  ifbieq2i  3682  ifbieq12i  3684  pweqi  3727  pwid  3736  sneqi  3746  elpr  3752  elsnc  3757  elsnc2  3763  ralsn  3768  rexsn  3769  eltp  3772  r19.12sn  3790  preq1i  3803  preq2i  3804  prid1  3828  snnz  3835  prnz  3836  tpnz  3838  sneqb  3877  unieqi  3902  unissi  3915  unidif  3924  inteqi  3931  intmin2  3954  intab  3957  intsn  3963  iinconst  3979  iuniin  3980  iinss1  3982  iunxdif2  4015  ssiinf  4016  iinss  4018  iinss2  4019  iinab  4028  iinun2  4033  iundif2  4034  iindif2  4036  iinin2  4037  iinxprg  4044  iunxsn  4046  iinuni  4050  iinpw  4055  opkeq1i  4063  opkeq2i  4064  complex  4105  snelpw  4116  snel1c  4141  eluni1  4174  xpkeq1i  4202  xpkeq2i  4203  opkabssvvk  4209  cnvkeqi  4217  ins2keqi  4221  ins3keqi  4222  imakeq1i  4227  imakeq2i  4228  cokeq1i  4233  cokeq2i  4234  p6eqi  4240  sikeqi  4243  elimak  4260  elimakv  4261  elp6  4264  sikss1c1c  4268  ins2kss  4280  ins3kss  4281  cnvkexg  4287  cnvkex  4288  p6exg  4291  dfuni12  4292  uni1ex  4294  ssetkex  4295  sikexg  4297  sikex  4298  dfimak2  4299  pw1ex  4304  ins2kexg  4306  ins3kexg  4307  ins2kex  4308  ins3kex  4309  imagekex  4313  uniex  4318  intex  4321  abexv  4325  pwex  4330  iotaval  4351  iota4an  4359  addceq1i  4387  addceq2i  4388  0nelsuc  4401  1cnnc  4409  nndisjeq  4430  leltfintr  4459  tfinnul  4492  tfin0c  4498  tfin1c  4500  0ceven  4506  tncveqnc1fin  4545  vfintle  4547  vfin1cltv  4548  vfinspsslem1  4551  nulnnn  4557  phiex  4573  opeq1i  4582  opeq2i  4583  proj1ex  4594  proj2ex  4595  mosubop  4614  phialllem2  4618  phiall  4619  opabbii  4627  breqi  4646  breq1i  4647  breq2i  4648  ssbri  4682  brab1  4685  opelopabf  4712  siex  4754  xpeq1i  4805  xpeq2i  4806  ssopr  4847  ideq  4871  coeq1i  4877  coeq2i  4878  cnveqi  4888  dmeqi  4909  dmv  4921  reseq1i  4931  reseq2i  4932  imaeq1i  4940  imaeq2i  4941  rneqi  4958  residm  4995  resdm  4999  resid  5006  ssrnres  5060  dmsnop  5070  cnvex  5103  dmex  5107  rnex  5108  cnviin  5119  funeqi  5129  funres  5144  funin  5164  funcnvres  5166  cnvresid  5167  fneq1i  5179  fneq2i  5180  fnresi  5201  dmopab2  5210  feq1i  5218  feq2i  5219  fdmi  5228  fssres  5239  fint  5246  foimacnv  5304  resdif  5307  resin  5308  f1ococnv2  5310  fveq1i  5330  fveq2i  5332  fv01  5355  fnressn  5439  fressnfv  5440  fvsnun1  5448  fvsnun2  5449  fconst2  5455  funiunfv  5468  isores1  5495  1stfo  5506  2ndfo  5507  swapf1o  5512  swapres  5513  opfv1st  5515  opfv2nd  5516  rnsi  5522  dmep  5525  oveq1i  5534  oveq2i  5535  oveqi  5537  oprabbii  5566  funoprab  5585  fnoprab  5587  fovcl  5589  ovidig  5594  ovigg  5597  caovmo  5646  dmmpti  5692  mpt2mpt  5710  fnmpt2i  5734  dmmpt2  5735  fixex  5790  ins2ex  5798  ins3ex  5799  imageex  5802  txpcofun  5804  brfns  5834  dmcross  5848  pw1fnval  5852  fnfullfun  5859  fullfunex  5861  fvfullfunlem3  5864  fvfullfun  5865  brfullfun  5867  dfnnc3  5886  eqerlem  5961  elqs  5978  ecqs  5989  map0  6026  mapsn  6027  enrflx  6036  dmen  6042  xpcomen  6053  xpassen  6058  enmap2lem3  6066  enmap1lem3  6072  enpw1pw  6076  enprmaplem3  6079  enprmaplem5  6081  enprmaplem6  6082  nceqi  6110  ncex  6118  nulnnc  6119  ncelncsi  6122  ncid  6124  eqnc  6128  1cnc  6140  df1c3  6141  ncaddccl  6145  ncdisjeq  6149  ncpw1c  6155  1p1e2c  6156  2p1e3c  6157  tc0c  6164  tcdi  6165  tc1c  6166  tc2c  6167  2nnc  6168  2nc  6169  ce0addcnnul  6180  ce0nnulb  6183  ce0nulnc  6185  ce2  6193  ce2nc1  6194  ce2ncpw11c  6195  lec0cg  6199  sbthlem1  6204  dflec2  6211  leconnnc  6219  ce2lt  6221  dflec3  6222  tcnc  6226  taddc  6230  letc  6232  ce2le  6234  cet  6235  tce2  6237  ce0lenc1  6240  brtcfn  6247  0lt1c  6259  nmembers1  6272  nncdiv3  6278  nchoicelem1  6290  nchoicelem5  6294  nchoicelem8  6297  nchoicelem9  6298  nchoicelem13  6302  nchoicelem17  6306  nchoicelem18  6307  nchoicelem19  6308  frecex  6314  frecxp  6315  fnfreclem2  6319  fnfreclem3  6320