Description: This theorem can be used
to eliminate a distinct variable restriction on
 and and  and replace it with the
"distinctor" and replace it with the
"distinctor"  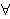   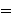  as an antecedent.
as an antecedent.  normally has normally has  free and can be read free and can be read
 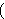  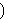 , and , and  substitutes
substitutes  for for  and can be read and can be read
 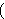  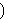 . We don't require that . We don't require that  and and  be distinct: if
they aren't, the distinctor will become false (in multiple-element
domains of discourse) and "protect" the consequent. be distinct: if
they aren't, the distinctor will become false (in multiple-element
domains of discourse) and "protect" the consequent.
To obtain a closed-theorem form of this inference, prefix the hypotheses
with 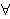  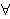  , conjoin them, and apply dvelimdf 2082. , conjoin them, and apply dvelimdf 2082.
Other variants of this theorem are dvelimh 1964 (with no distinct variable
restrictions), dvelimhw 1849 (that avoids ax-12 1925), and dvelimALT 2133 (that
avoids ax-10 2140). (Contributed by NM,
23-Nov-1994.) |