Description: Multiplication is an
operation on the complex numbers. This axiom tells
us that 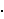 is
defined only on complex numbers which is analogous to
the way that other operations are defined, for example see subf 8423
or
eff 12287. However, while Metamath can handle this
axiom, if we wish to work
with weaker complex number axioms, we can avoid it by using the less
specific mulcl 8202. Note that uses of ax-mulf 8198 can be eliminated by using
the defined operation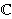      
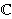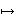
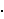 in place
of
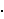, as seen in mpomulf 8212.
This axiom is justified by Theorem axmulf 8132. (New usage is discouraged.)
(Contributed by NM, 19-Oct-2004.) |
