Description: An alternate definition
of double existential uniqueness (see 2eu4 2287).
A mistake sometimes made in the literature is to use 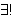  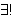  to
mean "exactly one to
mean "exactly one  and exactly one and exactly one  ." (For example, see
Proposition 7.53 of [TakeutiZaring] p. 53.) It turns out that
this is
actually a weaker assertion, as can be seen by expanding out the formal
definitions. This theorem shows that the erroneous definition can be
repaired by conjoining ." (For example, see
Proposition 7.53 of [TakeutiZaring] p. 53.) It turns out that
this is
actually a weaker assertion, as can be seen by expanding out the formal
definitions. This theorem shows that the erroneous definition can be
repaired by conjoining 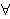  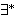   as an additional condition. The
correct definition apparently has never been published. ( as an additional condition. The
correct definition apparently has never been published. (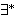 means
"there exists at most one".) (Contributed by NM,
26-Oct-2003.) means
"there exists at most one".) (Contributed by NM,
26-Oct-2003.) |