Theorem 2eu6 2289

Description: Two equivalent expressions for double existential uniqueness. (Contributed by NM, 2-Feb-2005.) (Revised by Mario Carneiro, 17-Oct-2016.)

Assertion

Ref	Expression
2eu6	|- ((E!xE.yph /\ E!yE.xph) <-> E.zE.wA.xA.y(ph <-> (x = z /\ y = w)))

Distinct variable groups:   x,y,z,w   ph,z,w

Allowed substitution hints:   ph(x,y)

Proof of Theorem 2eu6

Dummy variables v u are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		2eu4 2287	. 2 |- ((E!xE.yph /\ E!yE.xph) <-> (E.xE.yph /\ E.zE.wA.xA.y(ph -> (x = z /\ y = w))))
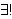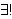
2		nfv 1619	. . . . . 6 |- F/zph
3		nfv 1619	. . . . . 6 |- F/wph
4		nfs1v 2106	. . . . . 6 |- F/x[z / x][w / y]ph
5		nfs1v 2106	. . . . . . 7 |- F/y[w / y]ph
6	5	nfsb 2109	. . . . . 6 |- F/y[z / x][w / y]ph
7		sbequ12 1919	. . . . . . 7 |- (y = w -> (ph <-> [w / y]ph))
8		sbequ12 1919	. . . . . . 7 |- (x = z -> ([w / y]ph <-> [z / x][w / y]ph))
9	7, 8	sylan9bbr 681	. . . . . 6 |- ((x = z /\ y = w) -> (ph <-> [z / x][w / y]ph))
10	2, 3, 4, 6, 9	cbvex2 2005	. . . . 5 |- (E.xE.yph <-> E.zE.w[z / x][w / y]ph)
11		equequ2 1686	. . . . . . . . . 10 |- (z = v -> (x = z <-> x = v))
12		equequ2 1686	. . . . . . . . . 10 |- (w = u -> (y = w <-> y = u))
13	11, 12	bi2anan9 843	. . . . . . . . 9 |- ((z = v /\ w = u) -> ((x = z /\ y = w) <-> (x = v /\ y = u)))
14	13	imbi2d 307	. . . . . . . 8 |- ((z = v /\ w = u) -> ((ph -> (x = z /\ y = w)) <-> (ph -> (x = v /\ y = u))))
15	14	2albidv 1627	. . . . . . 7 |- ((z = v /\ w = u) -> (A.xA.y(ph -> (x = z /\ y = w)) <-> A.xA.y(ph -> (x = v /\ y = u))))
16	15	cbvex2v 2007	. . . . . 6 |- (E.zE.wA.xA.y(ph -> (x = z /\ y = w)) <-> E.vE.uA.xA.y(ph -> (x = v /\ y = u)))
17		nfv 1619	. . . . . . . . 9 |- F/z(ph -> (x = v /\ y = u))
18		nfv 1619	. . . . . . . . 9 |- F/w(ph -> (x = v /\ y = u))
19		nfv 1619	. . . . . . . . . 10 |- F/x(z = v /\ w = u)
20	4, 19	nfim 1813	. . . . . . . . 9 |- F/x([z / x][w / y]ph -> (z = v /\ w = u))
21		nfv 1619	. . . . . . . . . 10 |- F/y(z = v /\ w = u)
22	6, 21	nfim 1813	. . . . . . . . 9 |- F/y([z / x][w / y]ph -> (z = v /\ w = u))
23		equequ1 1684	. . . . . . . . . . 11 |- (x = z -> (x = v <-> z = v))
24		equequ1 1684	. . . . . . . . . . 11 |- (y = w -> (y = u <-> w = u))
25	23, 24	bi2anan9 843	. . . . . . . . . 10 |- ((x = z /\ y = w) -> ((x = v /\ y = u) <-> (z = v /\ w = u)))
26	9, 25	imbi12d 311	. . . . . . . . 9 |- ((x = z /\ y = w) -> ((ph -> (x = v /\ y = u)) <-> ([z / x][w / y]ph -> (z = v /\ w = u))))
27	17, 18, 20, 22, 26	cbval2 2004	. . . . . . . 8 |- (A.xA.y(ph -> (x = v /\ y = u)) <-> A.zA.w([z / x][w / y]ph -> (z = v /\ w = u)))
28	27	2exbii 1583	. . . . . . 7 |- (E.vE.uA.xA.y(ph -> (x = v /\ y = u)) <-> E.vE.uA.zA.w([z / x][w / y]ph -> (z = v /\ w = u)))
29		2mo 2282	. . . . . . 7 |- (E.vE.uA.zA.w([z / x][w / y]ph -> (z = v /\ w = u)) <-> A.zA.wA.vA.u(([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u)))
30	28, 29	bitri 240	. . . . . 6 |- (E.vE.uA.xA.y(ph -> (x = v /\ y = u)) <-> A.zA.wA.vA.u(([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u)))
31	16, 30	bitri 240	. . . . 5 |- (E.zE.wA.xA.y(ph -> (x = z /\ y = w)) <-> A.zA.wA.vA.u(([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u)))
32		19.29r2 1598	. . . . 5 |- ((E.zE.w[z / x][w / y]ph /\ A.zA.wA.vA.u(([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u))) -> E.zE.w([z / x][w / y]ph /\ A.vA.u(([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u))))
33	10, 31, 32	syl2anb 465	. . . 4 |- ((E.xE.yph /\ E.zE.wA.xA.y(ph -> (x = z /\ y = w))) -> E.zE.w([z / x][w / y]ph /\ A.vA.u(([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u))))
34		2albiim 1612	. . . . . . 7 |- (A.xA.y(ph <-> (x = z /\ y = w)) <-> (A.xA.y(ph -> (x = z /\ y = w)) /\ A.xA.y((x = z /\ y = w) -> ph)))
35		ancom 437	. . . . . . 7 |- ((A.xA.y(ph -> (x = z /\ y = w)) /\ A.xA.y((x = z /\ y = w) -> ph)) <-> (A.xA.y((x = z /\ y = w) -> ph) /\ A.xA.y(ph -> (x = z /\ y = w))))
36	34, 35	bitri 240	. . . . . 6 |- (A.xA.y(ph <-> (x = z /\ y = w)) <-> (A.xA.y((x = z /\ y = w) -> ph) /\ A.xA.y(ph -> (x = z /\ y = w))))
37	36	2exbii 1583	. . . . 5 |- (E.zE.wA.xA.y(ph <-> (x = z /\ y = w)) <-> E.zE.w(A.xA.y((x = z /\ y = w) -> ph) /\ A.xA.y(ph -> (x = z /\ y = w))))
38		nfv 1619	. . . . . . . . . . . 12 |- F/v(([z / x][w / y]ph /\ ph) -> (z = x /\ w = y))
39		nfv 1619	. . . . . . . . . . . 12 |- F/u(([z / x][w / y]ph /\ ph) -> (z = x /\ w = y))
40	4	nfsb 2109	. . . . . . . . . . . . . . 15 |- F/x[u / w][z / x][w / y]ph
41	40	nfsb 2109	. . . . . . . . . . . . . 14 |- F/x[v / z][u / w][z / x][w / y]ph
42	4, 41	nfan 1824	. . . . . . . . . . . . 13 |- F/x([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph)
43	42, 19	nfim 1813	. . . . . . . . . . . 12 |- F/x(([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u))
44	6	nfsb 2109	. . . . . . . . . . . . . . 15 |- F/y[u / w][z / x][w / y]ph
45	44	nfsb 2109	. . . . . . . . . . . . . 14 |- F/y[v / z][u / w][z / x][w / y]ph
46	6, 45	nfan 1824	. . . . . . . . . . . . 13 |- F/y([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph)
47	46, 21	nfim 1813	. . . . . . . . . . . 12 |- F/y(([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u))
48		sbequ12 1919	. . . . . . . . . . . . . . . 16 |- (y = u -> (ph <-> [u / y]ph))
49		sbequ12 1919	. . . . . . . . . . . . . . . 16 |- (x = v -> ([u / y]ph <-> [v / x][u / y]ph))
50	48, 49	sylan9bbr 681	. . . . . . . . . . . . . . 15 |- ((x = v /\ y = u) -> (ph <-> [v / x][u / y]ph))
51	3	sbco2 2086	. . . . . . . . . . . . . . . . 17 |- ([u / w][w / y]ph <-> [u / y]ph)
52	51	sbbii 1653	. . . . . . . . . . . . . . . 16 |- ([v / x][u / w][w / y]ph <-> [v / x][u / y]ph)
53		nfv 1619	. . . . . . . . . . . . . . . . . 18 |- F/z[u / w][w / y]ph
54	53	sbco2 2086	. . . . . . . . . . . . . . . . 17 |- ([v / z][z / x][u / w][w / y]ph <-> [v / x][u / w][w / y]ph)
55		sbcom2 2114	. . . . . . . . . . . . . . . . . 18 |- ([z / x][u / w][w / y]ph <-> [u / w][z / x][w / y]ph)
56	55	sbbii 1653	. . . . . . . . . . . . . . . . 17 |- ([v / z][z / x][u / w][w / y]ph <-> [v / z][u / w][z / x][w / y]ph)
57	54, 56	bitr3i 242	. . . . . . . . . . . . . . . 16 |- ([v / x][u / w][w / y]ph <-> [v / z][u / w][z / x][w / y]ph)
58	52, 57	bitr3i 242	. . . . . . . . . . . . . . 15 |- ([v / x][u / y]ph <-> [v / z][u / w][z / x][w / y]ph)
59	50, 58	syl6bb 252	. . . . . . . . . . . . . 14 |- ((x = v /\ y = u) -> (ph <-> [v / z][u / w][z / x][w / y]ph))
60	59	anbi2d 684	. . . . . . . . . . . . 13 |- ((x = v /\ y = u) -> (([z / x][w / y]ph /\ ph) <-> ([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph)))
61		equequ2 1686	. . . . . . . . . . . . . 14 |- (x = v -> (z = x <-> z = v))
62		equequ2 1686	. . . . . . . . . . . . . 14 |- (y = u -> (w = y <-> w = u))
63	61, 62	bi2anan9 843	. . . . . . . . . . . . 13 |- ((x = v /\ y = u) -> ((z = x /\ w = y) <-> (z = v /\ w = u)))
64	60, 63	imbi12d 311	. . . . . . . . . . . 12 |- ((x = v /\ y = u) -> ((([z / x][w / y]ph /\ ph) -> (z = x /\ w = y)) <-> (([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u))))
65	38, 39, 43, 47, 64	cbval2 2004	. . . . . . . . . . 11 |- (A.xA.y(([z / x][w / y]ph /\ ph) -> (z = x /\ w = y)) <-> A.vA.u(([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u)))
66		equcom 1680	. . . . . . . . . . . . . . 15 |- (z = x <-> x = z)
67		equcom 1680	. . . . . . . . . . . . . . 15 |- (w = y <-> y = w)
68	66, 67	anbi12i 678	. . . . . . . . . . . . . 14 |- ((z = x /\ w = y) <-> (x = z /\ y = w))
69	68	imbi2i 303	. . . . . . . . . . . . 13 |- ((([z / x][w / y]ph /\ ph) -> (z = x /\ w = y)) <-> (([z / x][w / y]ph /\ ph) -> (x = z /\ y = w)))
70		impexp 433	. . . . . . . . . . . . 13 |- ((([z / x][w / y]ph /\ ph) -> (x = z /\ y = w)) <-> ([z / x][w / y]ph -> (ph -> (x = z /\ y = w))))
71	69, 70	bitri 240	. . . . . . . . . . . 12 |- ((([z / x][w / y]ph /\ ph) -> (z = x /\ w = y)) <-> ([z / x][w / y]ph -> (ph -> (x = z /\ y = w))))
72	71	2albii 1567	. . . . . . . . . . 11 |- (A.xA.y(([z / x][w / y]ph /\ ph) -> (z = x /\ w = y)) <-> A.xA.y([z / x][w / y]ph -> (ph -> (x = z /\ y = w))))
73	65, 72	bitr3i 242	. . . . . . . . . 10 |- (A.vA.u(([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u)) <-> A.xA.y([z / x][w / y]ph -> (ph -> (x = z /\ y = w))))
74	4, 6	19.21-2 1864	. . . . . . . . . 10 |- (A.xA.y([z / x][w / y]ph -> (ph -> (x = z /\ y = w))) <-> ([z / x][w / y]ph -> A.xA.y(ph -> (x = z /\ y = w))))
75	73, 74	bitri 240	. . . . . . . . 9 |- (A.vA.u(([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u)) <-> ([z / x][w / y]ph -> A.xA.y(ph -> (x = z /\ y = w))))
76	75	anbi2i 675	. . . . . . . 8 |- (([z / x][w / y]ph /\ A.vA.u(([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u))) <-> ([z / x][w / y]ph /\ ([z / x][w / y]ph -> A.xA.y(ph -> (x = z /\ y = w)))))
77		abai 770	. . . . . . . 8 |- (([z / x][w / y]ph /\ A.xA.y(ph -> (x = z /\ y = w))) <-> ([z / x][w / y]ph /\ ([z / x][w / y]ph -> A.xA.y(ph -> (x = z /\ y = w)))))
78	76, 77	bitr4i 243	. . . . . . 7 |- (([z / x][w / y]ph /\ A.vA.u(([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u))) <-> ([z / x][w / y]ph /\ A.xA.y(ph -> (x = z /\ y = w))))
79		2sb6 2113	. . . . . . . 8 |- ([z / x][w / y]ph <-> A.xA.y((x = z /\ y = w) -> ph))
80	79	anbi1i 676	. . . . . . 7 |- (([z / x][w / y]ph /\ A.xA.y(ph -> (x = z /\ y = w))) <-> (A.xA.y((x = z /\ y = w) -> ph) /\ A.xA.y(ph -> (x = z /\ y = w))))
81	78, 80	bitri 240	. . . . . 6 |- (([z / x][w / y]ph /\ A.vA.u(([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u))) <-> (A.xA.y((x = z /\ y = w) -> ph) /\ A.xA.y(ph -> (x = z /\ y = w))))
82	81	2exbii 1583	. . . . 5 |- (E.zE.w([z / x][w / y]ph /\ A.vA.u(([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u))) <-> E.zE.w(A.xA.y((x = z /\ y = w) -> ph) /\ A.xA.y(ph -> (x = z /\ y = w))))
83	37, 82	bitr4i 243	. . . 4 |- (E.zE.wA.xA.y(ph <-> (x = z /\ y = w)) <-> E.zE.w([z / x][w / y]ph /\ A.vA.u(([z / x][w / y]ph /\ [v / z][u / w][z / x][w / y]ph) -> (z = v /\ w = u))))
84	33, 83	sylibr 203	. . 3 |- ((E.xE.yph /\ E.zE.wA.xA.y(ph -> (x = z /\ y = w))) -> E.zE.wA.xA.y(ph <-> (x = z /\ y = w)))
85		bi2 189	. . . . . . 7 |- ((ph <-> (x = z /\ y = w)) -> ((x = z /\ y = w) -> ph))
86	85	2alimi 1560	. . . . . 6 |- (A.xA.y(ph <-> (x = z /\ y = w)) -> A.xA.y((x = z /\ y = w) -> ph))
87	86	2eximi 1577	. . . . 5 |- (E.zE.wA.xA.y(ph <-> (x = z /\ y = w)) -> E.zE.wA.xA.y((x = z /\ y = w) -> ph))
88		2exsb 2132	. . . . 5 |- (E.xE.yph <-> E.zE.wA.xA.y((x = z /\ y = w) -> ph))
89	87, 88	sylibr 203	. . . 4 |- (E.zE.wA.xA.y(ph <-> (x = z /\ y = w)) -> E.xE.yph)
90		bi1 178	. . . . . 6 |- ((ph <-> (x = z /\ y = w)) -> (ph -> (x = z /\ y = w)))
91	90	2alimi 1560	. . . . 5 |- (A.xA.y(ph <-> (x = z /\ y = w)) -> A.xA.y(ph -> (x = z /\ y = w)))
92	91	2eximi 1577	. . . 4 |- (E.zE.wA.xA.y(ph <-> (x = z /\ y = w)) -> E.zE.wA.xA.y(ph -> (x = z /\ y = w)))
93	89, 92	jca 518	. . 3 |- (E.zE.wA.xA.y(ph <-> (x = z /\ y = w)) -> (E.xE.yph /\ E.zE.wA.xA.y(ph -> (x = z /\ y = w))))
94	84, 93	impbii 180	. 2 |- ((E.xE.yph /\ E.zE.wA.xA.y(ph -> (x = z /\ y = w))) <-> E.zE.wA.xA.y(ph <-> (x = z /\ y = w)))
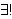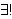95	1, 94	bitri 240	1 |- ((E!xE.yph /\ E!yE.xph) <-> E.zE.wA.xA.y(ph <-> (x = z /\ y = w)))

Syntax hints:   -> wi 4   <-> wb 176   /\ wa 358  A.wal 1540  E.wex 1541   = wceq 1642  [wsb 1648  E!weu 2204

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1546  ax-5 1557  ax-17 1616  ax-9 1654  ax-8 1675  ax-6 1729  ax-7 1734  ax-11 1746  ax-12 1925

This theorem depends on definitions:  df-bi 177  df-or 359  df-an 360  df-tru 1319  df-ex 1542  df-nf 1545  df-sb 1649  df-eu 2208

This theorem is referenced by: (None)