Theorem dfplpq2 7295

Description: Alternate definition of pre-addition on positive fractions. (Contributed by Jim Kingdon, 12-Sep-2019.)

Assertion

Ref	Expression
dfplpq2	|- +pQ = { <. <. x , y >. , z >. | ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ E. w E. v E. u E. f ( ( x = <. w , v >. /\ y = <. u , f >. ) /\ z = <. ( ( w .N f ) +N ( v .N u ) ) , ( v .N f ) >. ) ) }

Distinct variable group:   x, y, z, w, v, u, f

Proof of Theorem dfplpq2

Step	Hyp	Ref	Expression
1		df-mpo 5847	. 2 |- ( x e. ( N. X. N. ) , y e. ( N. X. N. ) |-> <. ( ( ( 1st ` x ) .N ( 2nd ` y ) ) +N ( ( 1st ` y ) .N ( 2nd ` x ) ) ) , ( ( 2nd ` x ) .N ( 2nd ` y ) ) >. ) = { <. <. x , y >. , z >. | ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ z = <. ( ( ( 1st ` x ) .N ( 2nd ` y ) ) +N ( ( 1st ` y ) .N ( 2nd ` x ) ) ) , ( ( 2nd ` x ) .N ( 2nd ` y ) ) >. ) }
2		df-plpq 7285	. 2 |- +pQ = ( x e. ( N. X. N. ) , y e. ( N. X. N. ) |-> <. ( ( ( 1st ` x ) .N ( 2nd ` y ) ) +N ( ( 1st ` y ) .N ( 2nd ` x ) ) ) , ( ( 2nd ` x ) .N ( 2nd ` y ) ) >. )
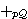
3		1st2nd2 6143	. . . . . . . . . 10 |- ( x e. ( N. X. N. ) -> x = <. ( 1st ` x ) , ( 2nd ` x ) >. )
4	3	eqeq1d 2174	. . . . . . . . 9 |- ( x e. ( N. X. N. ) -> ( x = <. w , v >. <-> <. ( 1st ` x ) , ( 2nd ` x ) >. = <. w , v >. ) )
5		1st2nd2 6143	. . . . . . . . . 10 |- ( y e. ( N. X. N. ) -> y = <. ( 1st ` y ) , ( 2nd ` y ) >. )
6	5	eqeq1d 2174	. . . . . . . . 9 |- ( y e. ( N. X. N. ) -> ( y = <. u , f >. <-> <. ( 1st ` y ) , ( 2nd ` y ) >. = <. u , f >. ) )
7	4, 6	bi2anan9 596	. . . . . . . 8 |- ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) -> ( ( x = <. w , v >. /\ y = <. u , f >. ) <-> ( <. ( 1st ` x ) , ( 2nd ` x ) >. = <. w , v >. /\ <. ( 1st ` y ) , ( 2nd ` y ) >. = <. u , f >. ) ) )
8	7	anbi1d 461	. . . . . . 7 |- ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) -> ( ( ( x = <. w , v >. /\ y = <. u , f >. ) /\ z = <. ( ( w .N f ) +N ( u .N v ) ) , ( v .N f ) >. ) <-> ( ( <. ( 1st ` x ) , ( 2nd ` x ) >. = <. w , v >. /\ <. ( 1st ` y ) , ( 2nd ` y ) >. = <. u , f >. ) /\ z = <. ( ( w .N f ) +N ( u .N v ) ) , ( v .N f ) >. ) ) )
9		xp1st 6133	. . . . . . . . . . . . . 14 |- ( y e. ( N. X. N. ) -> ( 1st ` y ) e. N. )
10	9	ad2antlr 481	. . . . . . . . . . . . 13 |- ( ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ ( x = <. w , v >. /\ y = <. u , f >. ) ) -> ( 1st ` y ) e. N. )
11	7	biimpa 294	. . . . . . . . . . . . . . 15 |- ( ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ ( x = <. w , v >. /\ y = <. u , f >. ) ) -> ( <. ( 1st ` x ) , ( 2nd ` x ) >. = <. w , v >. /\ <. ( 1st ` y ) , ( 2nd ` y ) >. = <. u , f >. ) )
12	11	simprd 113	. . . . . . . . . . . . . 14 |- ( ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ ( x = <. w , v >. /\ y = <. u , f >. ) ) -> <. ( 1st ` y ) , ( 2nd ` y ) >. = <. u , f >. )
13		vex 2729	. . . . . . . . . . . . . . . . 17 |- u e. _V
14		vex 2729	. . . . . . . . . . . . . . . . 17 |- f e. _V
15	13, 14	opth2 4218	. . . . . . . . . . . . . . . 16 |- ( <. ( 1st ` y ) , ( 2nd ` y ) >. = <. u , f >. <-> ( ( 1st ` y ) = u /\ ( 2nd ` y ) = f ) )
16	15	simplbi 272	. . . . . . . . . . . . . . 15 |- ( <. ( 1st ` y ) , ( 2nd ` y ) >. = <. u , f >. -> ( 1st ` y ) = u )
17	16	eleq1d 2235	. . . . . . . . . . . . . 14 |- ( <. ( 1st ` y ) , ( 2nd ` y ) >. = <. u , f >. -> ( ( 1st ` y ) e. N. <-> u e. N. ) )
18	12, 17	syl 14	. . . . . . . . . . . . 13 |- ( ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ ( x = <. w , v >. /\ y = <. u , f >. ) ) -> ( ( 1st ` y ) e. N. <-> u e. N. ) )
19	10, 18	mpbid 146	. . . . . . . . . . . 12 |- ( ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ ( x = <. w , v >. /\ y = <. u , f >. ) ) -> u e. N. )
20		xp2nd 6134	. . . . . . . . . . . . . 14 |- ( x e. ( N. X. N. ) -> ( 2nd ` x ) e. N. )
21	20	ad2antrr 480	. . . . . . . . . . . . 13 |- ( ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ ( x = <. w , v >. /\ y = <. u , f >. ) ) -> ( 2nd ` x ) e. N. )
22	11	simpld 111	. . . . . . . . . . . . . 14 |- ( ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ ( x = <. w , v >. /\ y = <. u , f >. ) ) -> <. ( 1st ` x ) , ( 2nd ` x ) >. = <. w , v >. )
23		vex 2729	. . . . . . . . . . . . . . . . 17 |- w e. _V
24		vex 2729	. . . . . . . . . . . . . . . . 17 |- v e. _V
25	23, 24	opth2 4218	. . . . . . . . . . . . . . . 16 |- ( <. ( 1st ` x ) , ( 2nd ` x ) >. = <. w , v >. <-> ( ( 1st ` x ) = w /\ ( 2nd ` x ) = v ) )
26	25	simprbi 273	. . . . . . . . . . . . . . 15 |- ( <. ( 1st ` x ) , ( 2nd ` x ) >. = <. w , v >. -> ( 2nd ` x ) = v )
27	26	eleq1d 2235	. . . . . . . . . . . . . 14 |- ( <. ( 1st ` x ) , ( 2nd ` x ) >. = <. w , v >. -> ( ( 2nd ` x ) e. N. <-> v e. N. ) )
28	22, 27	syl 14	. . . . . . . . . . . . 13 |- ( ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ ( x = <. w , v >. /\ y = <. u , f >. ) ) -> ( ( 2nd ` x ) e. N. <-> v e. N. ) )
29	21, 28	mpbid 146	. . . . . . . . . . . 12 |- ( ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ ( x = <. w , v >. /\ y = <. u , f >. ) ) -> v e. N. )
30		mulcompig 7272	. . . . . . . . . . . 12 |- ( ( u e. N. /\ v e. N. ) -> ( u .N v ) = ( v .N u ) )
31	19, 29, 30	syl2anc 409	. . . . . . . . . . 11 |- ( ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ ( x = <. w , v >. /\ y = <. u , f >. ) ) -> ( u .N v ) = ( v .N u ) )
32	31	oveq2d 5858	. . . . . . . . . 10 |- ( ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ ( x = <. w , v >. /\ y = <. u , f >. ) ) -> ( ( w .N f ) +N ( u .N v ) ) = ( ( w .N f ) +N ( v .N u ) ) )
33	32	opeq1d 3764	. . . . . . . . 9 |- ( ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ ( x = <. w , v >. /\ y = <. u , f >. ) ) -> <. ( ( w .N f ) +N ( u .N v ) ) , ( v .N f ) >. = <. ( ( w .N f ) +N ( v .N u ) ) , ( v .N f ) >. )
34	33	eqeq2d 2177	. . . . . . . 8 |- ( ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ ( x = <. w , v >. /\ y = <. u , f >. ) ) -> ( z = <. ( ( w .N f ) +N ( u .N v ) ) , ( v .N f ) >. <-> z = <. ( ( w .N f ) +N ( v .N u ) ) , ( v .N f ) >. ) )
35	34	pm5.32da 448	. . . . . . 7 |- ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) -> ( ( ( x = <. w , v >. /\ y = <. u , f >. ) /\ z = <. ( ( w .N f ) +N ( u .N v ) ) , ( v .N f ) >. ) <-> ( ( x = <. w , v >. /\ y = <. u , f >. ) /\ z = <. ( ( w .N f ) +N ( v .N u ) ) , ( v .N f ) >. ) ) )
36	8, 35	bitr3d 189	. . . . . 6 |- ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) -> ( ( ( <. ( 1st ` x ) , ( 2nd ` x ) >. = <. w , v >. /\ <. ( 1st ` y ) , ( 2nd ` y ) >. = <. u , f >. ) /\ z = <. ( ( w .N f ) +N ( u .N v ) ) , ( v .N f ) >. ) <-> ( ( x = <. w , v >. /\ y = <. u , f >. ) /\ z = <. ( ( w .N f ) +N ( v .N u ) ) , ( v .N f ) >. ) ) )
37	36	4exbidv 1858	. . . . 5 |- ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) -> ( E. w E. v E. u E. f ( ( <. ( 1st ` x ) , ( 2nd ` x ) >. = <. w , v >. /\ <. ( 1st ` y ) , ( 2nd ` y ) >. = <. u , f >. ) /\ z = <. ( ( w .N f ) +N ( u .N v ) ) , ( v .N f ) >. ) <-> E. w E. v E. u E. f ( ( x = <. w , v >. /\ y = <. u , f >. ) /\ z = <. ( ( w .N f ) +N ( v .N u ) ) , ( v .N f ) >. ) ) )
38		xp1st 6133	. . . . . . 7 |- ( x e. ( N. X. N. ) -> ( 1st ` x ) e. N. )
39	38, 20	jca 304	. . . . . 6 |- ( x e. ( N. X. N. ) -> ( ( 1st ` x ) e. N. /\ ( 2nd ` x ) e. N. ) )
40		xp2nd 6134	. . . . . . 7 |- ( y e. ( N. X. N. ) -> ( 2nd ` y ) e. N. )
41	9, 40	jca 304	. . . . . 6 |- ( y e. ( N. X. N. ) -> ( ( 1st ` y ) e. N. /\ ( 2nd ` y ) e. N. ) )
42		simpll 519	. . . . . . . . . . 11 |- ( ( ( w = ( 1st ` x ) /\ v = ( 2nd ` x ) ) /\ ( u = ( 1st ` y ) /\ f = ( 2nd ` y ) ) ) -> w = ( 1st ` x ) )
43		simprr 522	. . . . . . . . . . 11 |- ( ( ( w = ( 1st ` x ) /\ v = ( 2nd ` x ) ) /\ ( u = ( 1st ` y ) /\ f = ( 2nd ` y ) ) ) -> f = ( 2nd ` y ) )
44	42, 43	oveq12d 5860	. . . . . . . . . 10 |- ( ( ( w = ( 1st ` x ) /\ v = ( 2nd ` x ) ) /\ ( u = ( 1st ` y ) /\ f = ( 2nd ` y ) ) ) -> ( w .N f ) = ( ( 1st ` x ) .N ( 2nd ` y ) ) )
45		simprl 521	. . . . . . . . . . 11 |- ( ( ( w = ( 1st ` x ) /\ v = ( 2nd ` x ) ) /\ ( u = ( 1st ` y ) /\ f = ( 2nd ` y ) ) ) -> u = ( 1st ` y ) )
46		simplr 520	. . . . . . . . . . 11 |- ( ( ( w = ( 1st ` x ) /\ v = ( 2nd ` x ) ) /\ ( u = ( 1st ` y ) /\ f = ( 2nd ` y ) ) ) -> v = ( 2nd ` x ) )
47	45, 46	oveq12d 5860	. . . . . . . . . 10 |- ( ( ( w = ( 1st ` x ) /\ v = ( 2nd ` x ) ) /\ ( u = ( 1st ` y ) /\ f = ( 2nd ` y ) ) ) -> ( u .N v ) = ( ( 1st ` y ) .N ( 2nd ` x ) ) )
48	44, 47	oveq12d 5860	. . . . . . . . 9 |- ( ( ( w = ( 1st ` x ) /\ v = ( 2nd ` x ) ) /\ ( u = ( 1st ` y ) /\ f = ( 2nd ` y ) ) ) -> ( ( w .N f ) +N ( u .N v ) ) = ( ( ( 1st ` x ) .N ( 2nd ` y ) ) +N ( ( 1st ` y ) .N ( 2nd ` x ) ) ) )
49	46, 43	oveq12d 5860	. . . . . . . . 9 |- ( ( ( w = ( 1st ` x ) /\ v = ( 2nd ` x ) ) /\ ( u = ( 1st ` y ) /\ f = ( 2nd ` y ) ) ) -> ( v .N f ) = ( ( 2nd ` x ) .N ( 2nd ` y ) ) )
50	48, 49	opeq12d 3766	. . . . . . . 8 |- ( ( ( w = ( 1st ` x ) /\ v = ( 2nd ` x ) ) /\ ( u = ( 1st ` y ) /\ f = ( 2nd ` y ) ) ) -> <. ( ( w .N f ) +N ( u .N v ) ) , ( v .N f ) >. = <. ( ( ( 1st ` x ) .N ( 2nd ` y ) ) +N ( ( 1st ` y ) .N ( 2nd ` x ) ) ) , ( ( 2nd ` x ) .N ( 2nd ` y ) ) >. )
51	50	eqeq2d 2177	. . . . . . 7 |- ( ( ( w = ( 1st ` x ) /\ v = ( 2nd ` x ) ) /\ ( u = ( 1st ` y ) /\ f = ( 2nd ` y ) ) ) -> ( z = <. ( ( w .N f ) +N ( u .N v ) ) , ( v .N f ) >. <-> z = <. ( ( ( 1st ` x ) .N ( 2nd ` y ) ) +N ( ( 1st ` y ) .N ( 2nd ` x ) ) ) , ( ( 2nd ` x ) .N ( 2nd ` y ) ) >. ) )
52	51	copsex4g 4225	. . . . . 6 |- ( ( ( ( 1st ` x ) e. N. /\ ( 2nd ` x ) e. N. ) /\ ( ( 1st ` y ) e. N. /\ ( 2nd ` y ) e. N. ) ) -> ( E. w E. v E. u E. f ( ( <. ( 1st ` x ) , ( 2nd ` x ) >. = <. w , v >. /\ <. ( 1st ` y ) , ( 2nd ` y ) >. = <. u , f >. ) /\ z = <. ( ( w .N f ) +N ( u .N v ) ) , ( v .N f ) >. ) <-> z = <. ( ( ( 1st ` x ) .N ( 2nd ` y ) ) +N ( ( 1st ` y ) .N ( 2nd ` x ) ) ) , ( ( 2nd ` x ) .N ( 2nd ` y ) ) >. ) )
53	39, 41, 52	syl2an 287	. . . . 5 |- ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) -> ( E. w E. v E. u E. f ( ( <. ( 1st ` x ) , ( 2nd ` x ) >. = <. w , v >. /\ <. ( 1st ` y ) , ( 2nd ` y ) >. = <. u , f >. ) /\ z = <. ( ( w .N f ) +N ( u .N v ) ) , ( v .N f ) >. ) <-> z = <. ( ( ( 1st ` x ) .N ( 2nd ` y ) ) +N ( ( 1st ` y ) .N ( 2nd ` x ) ) ) , ( ( 2nd ` x ) .N ( 2nd ` y ) ) >. ) )
54	37, 53	bitr3d 189	. . . 4 |- ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) -> ( E. w E. v E. u E. f ( ( x = <. w , v >. /\ y = <. u , f >. ) /\ z = <. ( ( w .N f ) +N ( v .N u ) ) , ( v .N f ) >. ) <-> z = <. ( ( ( 1st ` x ) .N ( 2nd ` y ) ) +N ( ( 1st ` y ) .N ( 2nd ` x ) ) ) , ( ( 2nd ` x ) .N ( 2nd ` y ) ) >. ) )
55	54	pm5.32i 450	. . 3 |- ( ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ E. w E. v E. u E. f ( ( x = <. w , v >. /\ y = <. u , f >. ) /\ z = <. ( ( w .N f ) +N ( v .N u ) ) , ( v .N f ) >. ) ) <-> ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ z = <. ( ( ( 1st ` x ) .N ( 2nd ` y ) ) +N ( ( 1st ` y ) .N ( 2nd ` x ) ) ) , ( ( 2nd ` x ) .N ( 2nd ` y ) ) >. ) )
56	55	oprabbii 5897	. 2 |- { <. <. x , y >. , z >. | ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ E. w E. v E. u E. f ( ( x = <. w , v >. /\ y = <. u , f >. ) /\ z = <. ( ( w .N f ) +N ( v .N u ) ) , ( v .N f ) >. ) ) } = { <. <. x , y >. , z >. | ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ z = <. ( ( ( 1st ` x ) .N ( 2nd ` y ) ) +N ( ( 1st ` y ) .N ( 2nd ` x ) ) ) , ( ( 2nd ` x ) .N ( 2nd ` y ) ) >. ) }
57	1, 2, 56	3eqtr4i 2196	1 |- +pQ = { <. <. x , y >. , z >. | ( ( x e. ( N. X. N. ) /\ y e. ( N. X. N. ) ) /\ E. w E. v E. u E. f ( ( x = <. w , v >. /\ y = <. u , f >. ) /\ z = <. ( ( w .N f ) +N ( v .N u ) ) , ( v .N f ) >. ) ) }

Syntax hints:   /\ wa 103   <-> wb 104   = wceq 1343   E.wex 1480   e. wcel 2136   <.cop 3579   X. cxp 4602   ` cfv 5188  (class class class)co 5842   {coprab 5843   e. cmpo 5844   1stc1st 6106   2ndc2nd 6107   N.cnpi 7213   +N cpli 7214   .N cmi 7215   +pQ cplpq 7217

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-ia1 105  ax-ia2 106  ax-ia3 107  ax-in1 604  ax-in2 605  ax-io 699  ax-5 1435  ax-7 1436  ax-gen 1437  ax-ie1 1481  ax-ie2 1482  ax-8 1492  ax-10 1493  ax-11 1494  ax-i12 1495  ax-bndl 1497  ax-4 1498  ax-17 1514  ax-i9 1518  ax-ial 1522  ax-i5r 1523  ax-13 2138  ax-14 2139  ax-ext 2147  ax-coll 4097  ax-sep 4100  ax-nul 4108  ax-pow 4153  ax-pr 4187  ax-un 4411  ax-setind 4514  ax-iinf 4565

This theorem depends on definitions:  df-bi 116  df-3an 970  df-tru 1346  df-fal 1349  df-nf 1449  df-sb 1751  df-eu 2017  df-mo 2018  df-clab 2152  df-cleq 2158  df-clel 2161  df-nfc 2297  df-ne 2337  df-ral 2449  df-rex 2450  df-reu 2451  df-rab 2453  df-v 2728  df-sbc 2952  df-csb 3046  df-dif 3118  df-un 3120  df-in 3122  df-ss 3129  df-nul 3410  df-pw 3561  df-sn 3582  df-pr 3583  df-op 3585  df-uni 3790  df-int 3825  df-iun 3868  df-br 3983  df-opab 4044  df-mpt 4045  df-tr 4081  df-id 4271  df-iord 4344  df-on 4346  df-suc 4349  df-iom 4568  df-xp 4610  df-rel 4611  df-cnv 4612  df-co 4613  df-dm 4614  df-rn 4615  df-res 4616  df-ima 4617  df-iota 5153  df-fun 5190  df-fn 5191  df-f 5192  df-f1 5193  df-fo 5194  df-f1o 5195  df-fv 5196  df-ov 5845  df-oprab 5846  df-mpo 5847  df-1st 6108  df-2nd 6109  df-recs 6273  df-irdg 6338  df-oadd 6388  df-omul 6389  df-ni 7245  df-mi 7247  df-plpq 7285

This theorem is referenced by:  addpipqqs  7311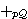