Description: Define the floor
(greatest integer less than or equal to) function. See
flval 10452 for its value, flqlelt 10456 for its basic property, and flqcl 10453 for
its closure. For example,  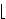   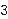 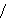 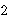    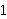 while while
 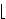    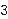 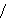 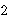     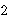 (ex-fl 15861). (ex-fl 15861).
Although we define this on real numbers so that notations are similar to
the Metamath Proof Explorer, in the absence of excluded middle few
theorems will be possible for all real numbers. Imagine a real number
which is around 2.99995 or 3.00001 . In order to determine whether its
floor is 2 or 3, it would be necessary to compute the number to
arbitrary precision.
The term "floor" was coined by Ken Iverson. He also invented
a
mathematical notation for floor, consisting of an L-shaped left bracket
and its reflection as a right bracket. In APL, the left-bracket alone
is used, and we borrow this idea. (Thanks to Paul Chapman for this
information.) (Contributed by NM,
14-Nov-2004.) |