Description: Define the slot extractor
for extensible structures. The class
Slot  is a
function whose argument can be any set, although it is
meaningful only if that set is a member of an extensible structure (such
as a partially ordered set or a group). is a
function whose argument can be any set, although it is
meaningful only if that set is a member of an extensible structure (such
as a partially ordered set or a group).
Note that Slot  is implemented as "evaluation at
is implemented as "evaluation at  ". That is, ". That is,
 Slot Slot   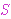  is
defined to be is
defined to be  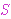    ,
where ,
where  will
typically be a small nonzero natural number. Each extensible structure will
typically be a small nonzero natural number. Each extensible structure
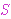 is a function
defined on specific natural number "slots", and this
function extracts the value at a particular slot. is a function
defined on specific natural number "slots", and this
function extracts the value at a particular slot.
The special "structure" 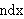 , defined as the identity function
restricted to , defined as the identity function
restricted to 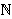 , can be used to extract the number , can be used to extract the number  from a
slot, since from a
slot, since  Slot Slot
  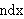  
 (see ndxarg 12970). This is
typically used to refer to the number of a slot when defining structures
without having to expose the detail of what that number is (for
instance, we use the expression (see ndxarg 12970). This is
typically used to refer to the number of a slot when defining structures
without having to expose the detail of what that number is (for
instance, we use the expression  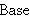  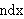  in theorems and
proofs instead of its value 1). in theorems and
proofs instead of its value 1).
The class Slot cannot be defined as
   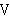 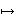    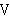 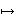        because each Slot because each Slot  is a function on the proper class
is a function on the proper class 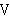 so is itself a proper class,
and the values of functions are sets (fvex 5619). It is necessary to
allow proper classes as values of Slot so is itself a proper class,
and the values of functions are sets (fvex 5619). It is necessary to
allow proper classes as values of Slot  since for instance the
class of all (base sets of) groups is proper. (Contributed by Mario
Carneiro, 22-Sep-2015.) since for instance the
class of all (base sets of) groups is proper. (Contributed by Mario
Carneiro, 22-Sep-2015.) |