Description: Define power class.
Definition 5.10 of [TakeutiZaring] p. 17,
but we
also let it apply to proper classes, i.e. those that are not members of
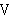 . When
applied to a set, this produces its power set. A power
set of S is the set of all subsets of S, including the empty set and S
itself. For example, if . When
applied to a set, this produces its power set. A power
set of S is the set of all subsets of S, including the empty set and S
itself. For example, if  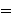 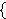 3 , 5 , 7 3 , 5 , 7 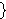 , then , then
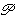  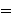 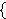 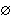  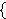 3 3 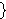  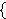 5 5 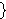  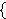 7 7 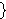  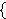 3 , 5 3 , 5
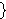 
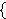 3 , 7 3 , 7 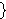  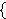 5 , 7 5 , 7 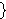  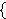 3 , 5 , 7 3 , 5 , 7 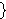 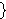 (ex-pw in
set.mm). We will later introduce the Axiom of Power Sets ax-pow in
set.mm, which can be expressed in class notation per pwexg 4329. Still
later we will prove, in hashpw in set.mm, that the size of the power set
of a finite set is 2 raised to the power of the size of the set.
(Contributed by NM, 5-Aug-1993.) (ex-pw in
set.mm). We will later introduce the Axiom of Power Sets ax-pow in
set.mm, which can be expressed in class notation per pwexg 4329. Still
later we will prove, in hashpw in set.mm, that the size of the power set
of a finite set is 2 raised to the power of the size of the set.
(Contributed by NM, 5-Aug-1993.) |