Theorem ivthinclemuopn 12785

Description: Lemma for ivthinc 12790. The upper cut is open. (Contributed by Jim Kingdon, 19-Feb-2024.)

Hypotheses

Ref	Expression
ivth.1	|- ( ph -> A e. RR )
ivth.2	|- ( ph -> B e. RR )
ivth.3	|- ( ph -> U e. RR )
ivth.4	|- ( ph -> A < B )
ivth.5	|- ( ph -> ( A [,] B ) C_ D )
ivth.7	|- ( ph -> F e. ( D -cn-> CC ) )
ivth.8	|- ( ( ph /\ x e. ( A [,] B ) ) -> ( F ` x ) e. RR )
ivth.9	|- ( ph -> ( ( F ` A ) < U /\ U < ( F ` B ) ) )
ivthinc.i	|- ( ( ( ph /\ x e. ( A [,] B ) ) /\ ( y e. ( A [,] B ) /\ x < y ) ) -> ( F ` x ) < ( F ` y ) )
ivthinclem.l	|- L = { w e. ( A [,] B ) | ( F ` w ) < U }
ivthinclem.r	|- R = { w e. ( A [,] B ) | U < ( F ` w ) }
ivthinclemuopn.r	|- ( ph -> S e. R )

Assertion

Ref	Expression
ivthinclemuopn	|- ( ph -> E. q e. R q < S )

Distinct variable groups:   w, A   x, A, y   w, B   x, B, y   w, F   x, F, y   R, q   S, q   w, S   x, S, y   w, U   ph, x, y

Allowed substitution hints:   ph( w, q)   A( q)   B( q)   D( x, y, w, q)   R( x, y, w)   U( x, y, q)   F( q)   L( x, y, w, q)

Proof of Theorem ivthinclemuopn

Dummy variables z d are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		ivth.7	. . 3 |- ( ph -> F e. ( D -cn-> CC ) )
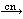2		ivth.5	. . . 4 |- ( ph -> ( A [,] B ) C_ D )
3		ivthinclemuopn.r	. . . . . 6 |- ( ph -> S e. R )
4		fveq2 5421	. . . . . . . 8 |- ( w = S -> ( F ` w ) = ( F ` S ) )
5	4	breq2d 3941	. . . . . . 7 |- ( w = S -> ( U < ( F ` w ) <-> U < ( F ` S ) ) )
6		ivthinclem.r	. . . . . . 7 |- R = { w e. ( A [,] B ) | U < ( F ` w ) }
7	5, 6	elrab2 2843	. . . . . 6 |- ( S e. R <-> ( S e. ( A [,] B ) /\ U < ( F ` S ) ) )
8	3, 7	sylib 121	. . . . 5 |- ( ph -> ( S e. ( A [,] B ) /\ U < ( F ` S ) ) )
9	8	simpld 111	. . . 4 |- ( ph -> S e. ( A [,] B ) )
10	2, 9	sseldd 3098	. . 3 |- ( ph -> S e. D )
11		fveq2 5421	. . . . . . 7 |- ( x = S -> ( F ` x ) = ( F ` S ) )
12	11	eleq1d 2208	. . . . . 6 |- ( x = S -> ( ( F ` x ) e. RR <-> ( F ` S ) e. RR ) )
13		ivth.8	. . . . . . 7 |- ( ( ph /\ x e. ( A [,] B ) ) -> ( F ` x ) e. RR )
14	13	ralrimiva 2505	. . . . . 6 |- ( ph -> A. x e. ( A [,] B ) ( F ` x ) e. RR )
15	12, 14, 9	rspcdva 2794	. . . . 5 |- ( ph -> ( F ` S ) e. RR )
16		ivth.3	. . . . 5 |- ( ph -> U e. RR )
17	15, 16	resubcld 8143	. . . 4 |- ( ph -> ( ( F ` S ) - U ) e. RR )
18	8	simprd 113	. . . . 5 |- ( ph -> U < ( F ` S ) )
19	16, 15	posdifd 8294	. . . . 5 |- ( ph -> ( U < ( F ` S ) <-> 0 < ( ( F ` S ) - U ) ) )
20	18, 19	mpbid 146	. . . 4 |- ( ph -> 0 < ( ( F ` S ) - U ) )
21	17, 20	elrpd 9481	. . 3 |- ( ph -> ( ( F ` S ) - U ) e. RR+ )
22		cncfi 12734	. . 3 |- ( ( F e. ( D -cn-> CC ) /\ S e. D /\ ( ( F ` S ) - U ) e. RR+ ) -> E. d e. RR+ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) )
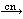
23	1, 10, 21, 22	syl3anc 1216	. 2 |- ( ph -> E. d e. RR+ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) )
24		ivth.1	. . . . . . . . . 10 |- ( ph -> A e. RR )
25		ivth.2	. . . . . . . . . 10 |- ( ph -> B e. RR )
26		elicc2 9721	. . . . . . . . . 10 |- ( ( A e. RR /\ B e. RR ) -> ( S e. ( A [,] B ) <-> ( S e. RR /\ A <_ S /\ S <_ B ) ) )
27	24, 25, 26	syl2anc 408	. . . . . . . . 9 |- ( ph -> ( S e. ( A [,] B ) <-> ( S e. RR /\ A <_ S /\ S <_ B ) ) )
28	9, 27	mpbid 146	. . . . . . . 8 |- ( ph -> ( S e. RR /\ A <_ S /\ S <_ B ) )
29	28	simp1d 993	. . . . . . 7 |- ( ph -> S e. RR )
30	29	adantr 274	. . . . . 6 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> S e. RR )
31		simprl 520	. . . . . . . 8 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> d e. RR+ )
32	31	rphalfcld 9496	. . . . . . 7 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( d / 2 ) e. RR+ )
33	32	rpred 9483	. . . . . 6 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( d / 2 ) e. RR )
34	30, 33	resubcld 8143	. . . . 5 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( S - ( d / 2 ) ) e. RR )
35	24	adantr 274	. . . . . 6 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> A e. RR )
36	31	rpred 9483	. . . . . . . 8 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> d e. RR )
37	30, 36	resubcld 8143	. . . . . . 7 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( S - d ) e. RR )
38	15	ad2antrr 479	. . . . . . . . . . . 12 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> ( F ` S ) e. RR )
39	38	recnd 7794	. . . . . . . . . . 11 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> ( F ` S ) e. CC )
40	16	recnd 7794	. . . . . . . . . . . 12 |- ( ph -> U e. CC )
41	40	ad2antrr 479	. . . . . . . . . . 11 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> U e. CC )
42	39, 41	nncand 8078	. . . . . . . . . 10 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> ( ( F ` S ) - ( ( F ` S ) - U ) ) = U )
43		simpr 109	. . . . . . . . . . . . . 14 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> ( S - d ) < A )
44	24	ad2antrr 479	. . . . . . . . . . . . . . 15 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> A e. RR )
45	29	ad2antrr 479	. . . . . . . . . . . . . . 15 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> S e. RR )
46	31	adantr 274	. . . . . . . . . . . . . . . . 17 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> d e. RR+ )
47	46	rpred 9483	. . . . . . . . . . . . . . . 16 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> d e. RR )
48	45, 47	readdcld 7795	. . . . . . . . . . . . . . 15 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> ( S + d ) e. RR )
49	28	simp2d 994	. . . . . . . . . . . . . . . 16 |- ( ph -> A <_ S )
50	49	ad2antrr 479	. . . . . . . . . . . . . . 15 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> A <_ S )
51	45, 46	ltaddrpd 9517	. . . . . . . . . . . . . . 15 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> S < ( S + d ) )
52	44, 45, 48, 50, 51	lelttrd 7887	. . . . . . . . . . . . . 14 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> A < ( S + d ) )
53	44, 45, 47	absdifltd 10950	. . . . . . . . . . . . . 14 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> ( ( abs ` ( A - S ) ) < d <-> ( ( S - d ) < A /\ A < ( S + d ) ) ) )
54	43, 52, 53	mpbir2and 928	. . . . . . . . . . . . 13 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> ( abs ` ( A - S ) ) < d )
55		fvoveq1 5797	. . . . . . . . . . . . . . . 16 |- ( z = A -> ( abs ` ( z - S ) ) = ( abs ` ( A - S ) ) )
56	55	breq1d 3939	. . . . . . . . . . . . . . 15 |- ( z = A -> ( ( abs ` ( z - S ) ) < d <-> ( abs ` ( A - S ) ) < d ) )
57	56	imbrov2fvoveq 5799	. . . . . . . . . . . . . 14 |- ( z = A -> ( ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) <-> ( ( abs ` ( A - S ) ) < d -> ( abs ` ( ( F ` A ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) )
58		simplrr 525	. . . . . . . . . . . . . 14 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) )
59	24	rexrd 7815	. . . . . . . . . . . . . . . . 17 |- ( ph -> A e. RR* )
60	25	rexrd 7815	. . . . . . . . . . . . . . . . 17 |- ( ph -> B e. RR* )
61		ivth.4	. . . . . . . . . . . . . . . . . 18 |- ( ph -> A < B )
62	24, 25, 61	ltled 7881	. . . . . . . . . . . . . . . . 17 |- ( ph -> A <_ B )
63		lbicc2 9767	. . . . . . . . . . . . . . . . 17 |- ( ( A e. RR* /\ B e. RR* /\ A <_ B ) -> A e. ( A [,] B ) )
64	59, 60, 62, 63	syl3anc 1216	. . . . . . . . . . . . . . . 16 |- ( ph -> A e. ( A [,] B ) )
65	2, 64	sseldd 3098	. . . . . . . . . . . . . . 15 |- ( ph -> A e. D )
66	65	ad2antrr 479	. . . . . . . . . . . . . 14 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> A e. D )
67	57, 58, 66	rspcdva 2794	. . . . . . . . . . . . 13 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> ( ( abs ` ( A - S ) ) < d -> ( abs ` ( ( F ` A ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) )
68	54, 67	mpd 13	. . . . . . . . . . . 12 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> ( abs ` ( ( F ` A ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) )
69		fveq2 5421	. . . . . . . . . . . . . . . 16 |- ( x = A -> ( F ` x ) = ( F ` A ) )
70	69	eleq1d 2208	. . . . . . . . . . . . . . 15 |- ( x = A -> ( ( F ` x ) e. RR <-> ( F ` A ) e. RR ) )
71	14	adantr 274	. . . . . . . . . . . . . . 15 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> A. x e. ( A [,] B ) ( F ` x ) e. RR )
72	64	adantr 274	. . . . . . . . . . . . . . 15 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> A e. ( A [,] B ) )
73	70, 71, 72	rspcdva 2794	. . . . . . . . . . . . . 14 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( F ` A ) e. RR )
74	73	adantr 274	. . . . . . . . . . . . 13 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> ( F ` A ) e. RR )
75	17	ad2antrr 479	. . . . . . . . . . . . 13 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> ( ( F ` S ) - U ) e. RR )
76	74, 38, 75	absdifltd 10950	. . . . . . . . . . . 12 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> ( ( abs ` ( ( F ` A ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) <-> ( ( ( F ` S ) - ( ( F ` S ) - U ) ) < ( F ` A ) /\ ( F ` A ) < ( ( F ` S ) + ( ( F ` S ) - U ) ) ) ) )
77	68, 76	mpbid 146	. . . . . . . . . . 11 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> ( ( ( F ` S ) - ( ( F ` S ) - U ) ) < ( F ` A ) /\ ( F ` A ) < ( ( F ` S ) + ( ( F ` S ) - U ) ) ) )
78	77	simpld 111	. . . . . . . . . 10 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> ( ( F ` S ) - ( ( F ` S ) - U ) ) < ( F ` A ) )
79	42, 78	eqbrtrrd 3952	. . . . . . . . 9 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> U < ( F ` A ) )
80	16	ad2antrr 479	. . . . . . . . . 10 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> U e. RR )
81		ivth.9	. . . . . . . . . . . 12 |- ( ph -> ( ( F ` A ) < U /\ U < ( F ` B ) ) )
82	81	simpld 111	. . . . . . . . . . 11 |- ( ph -> ( F ` A ) < U )
83	82	ad2antrr 479	. . . . . . . . . 10 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> ( F ` A ) < U )
84	74, 80, 83	ltnsymd 7882	. . . . . . . . 9 |- ( ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) /\ ( S - d ) < A ) -> -. U < ( F ` A ) )
85	79, 84	pm2.65da 650	. . . . . . . 8 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> -. ( S - d ) < A )
86	35, 37, 85	nltled 7883	. . . . . . 7 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> A <_ ( S - d ) )
87		rphalflt 9471	. . . . . . . . 9 |- ( d e. RR+ -> ( d / 2 ) < d )
88	31, 87	syl 14	. . . . . . . 8 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( d / 2 ) < d )
89	33, 36, 30, 88	ltsub2dd 8320	. . . . . . 7 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( S - d ) < ( S - ( d / 2 ) ) )
90	35, 37, 34, 86, 89	lelttrd 7887	. . . . . 6 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> A < ( S - ( d / 2 ) ) )
91	35, 34, 90	ltled 7881	. . . . 5 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> A <_ ( S - ( d / 2 ) ) )
92	25	adantr 274	. . . . . 6 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> B e. RR )
93	30, 32	ltsubrpd 9516	. . . . . . 7 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( S - ( d / 2 ) ) < S )
94	34, 30, 93	ltled 7881	. . . . . 6 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( S - ( d / 2 ) ) <_ S )
95	28	simp3d 995	. . . . . . 7 |- ( ph -> S <_ B )
96	95	adantr 274	. . . . . 6 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> S <_ B )
97	34, 30, 92, 94, 96	letrd 7886	. . . . 5 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( S - ( d / 2 ) ) <_ B )
98		elicc2 9721	. . . . . 6 |- ( ( A e. RR /\ B e. RR ) -> ( ( S - ( d / 2 ) ) e. ( A [,] B ) <-> ( ( S - ( d / 2 ) ) e. RR /\ A <_ ( S - ( d / 2 ) ) /\ ( S - ( d / 2 ) ) <_ B ) ) )
99	35, 92, 98	syl2anc 408	. . . . 5 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( ( S - ( d / 2 ) ) e. ( A [,] B ) <-> ( ( S - ( d / 2 ) ) e. RR /\ A <_ ( S - ( d / 2 ) ) /\ ( S - ( d / 2 ) ) <_ B ) ) )
100	34, 91, 97, 99	mpbir3and 1164	. . . 4 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( S - ( d / 2 ) ) e. ( A [,] B ) )
101		fveq2 5421	. . . . . . . . 9 |- ( x = ( S - ( d / 2 ) ) -> ( F ` x ) = ( F ` ( S - ( d / 2 ) ) ) )
102	101	eleq1d 2208	. . . . . . . 8 |- ( x = ( S - ( d / 2 ) ) -> ( ( F ` x ) e. RR <-> ( F ` ( S - ( d / 2 ) ) ) e. RR ) )
103	102, 71, 100	rspcdva 2794	. . . . . . 7 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( F ` ( S - ( d / 2 ) ) ) e. RR )
104	15	adantr 274	. . . . . . 7 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( F ` S ) e. RR )
105		breq2 3933	. . . . . . . . . . 11 |- ( y = S -> ( ( S - ( d / 2 ) ) < y <-> ( S - ( d / 2 ) ) < S ) )
106		fveq2 5421	. . . . . . . . . . . 12 |- ( y = S -> ( F ` y ) = ( F ` S ) )
107	106	breq2d 3941	. . . . . . . . . . 11 |- ( y = S -> ( ( F ` ( S - ( d / 2 ) ) ) < ( F ` y ) <-> ( F ` ( S - ( d / 2 ) ) ) < ( F ` S ) ) )
108	105, 107	imbi12d 233	. . . . . . . . . 10 |- ( y = S -> ( ( ( S - ( d / 2 ) ) < y -> ( F ` ( S - ( d / 2 ) ) ) < ( F ` y ) ) <-> ( ( S - ( d / 2 ) ) < S -> ( F ` ( S - ( d / 2 ) ) ) < ( F ` S ) ) ) )
109		breq1 3932	. . . . . . . . . . . . 13 |- ( x = ( S - ( d / 2 ) ) -> ( x < y <-> ( S - ( d / 2 ) ) < y ) )
110	101	breq1d 3939	. . . . . . . . . . . . 13 |- ( x = ( S - ( d / 2 ) ) -> ( ( F ` x ) < ( F ` y ) <-> ( F ` ( S - ( d / 2 ) ) ) < ( F ` y ) ) )
111	109, 110	imbi12d 233	. . . . . . . . . . . 12 |- ( x = ( S - ( d / 2 ) ) -> ( ( x < y -> ( F ` x ) < ( F ` y ) ) <-> ( ( S - ( d / 2 ) ) < y -> ( F ` ( S - ( d / 2 ) ) ) < ( F ` y ) ) ) )
112	111	ralbidv 2437	. . . . . . . . . . 11 |- ( x = ( S - ( d / 2 ) ) -> ( A. y e. ( A [,] B ) ( x < y -> ( F ` x ) < ( F ` y ) ) <-> A. y e. ( A [,] B ) ( ( S - ( d / 2 ) ) < y -> ( F ` ( S - ( d / 2 ) ) ) < ( F ` y ) ) ) )
113		ivthinc.i	. . . . . . . . . . . . . . 15 |- ( ( ( ph /\ x e. ( A [,] B ) ) /\ ( y e. ( A [,] B ) /\ x < y ) ) -> ( F ` x ) < ( F ` y ) )
114	113	expr 372	. . . . . . . . . . . . . 14 |- ( ( ( ph /\ x e. ( A [,] B ) ) /\ y e. ( A [,] B ) ) -> ( x < y -> ( F ` x ) < ( F ` y ) ) )
115	114	ralrimiva 2505	. . . . . . . . . . . . 13 |- ( ( ph /\ x e. ( A [,] B ) ) -> A. y e. ( A [,] B ) ( x < y -> ( F ` x ) < ( F ` y ) ) )
116	115	ralrimiva 2505	. . . . . . . . . . . 12 |- ( ph -> A. x e. ( A [,] B ) A. y e. ( A [,] B ) ( x < y -> ( F ` x ) < ( F ` y ) ) )
117	116	adantr 274	. . . . . . . . . . 11 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> A. x e. ( A [,] B ) A. y e. ( A [,] B ) ( x < y -> ( F ` x ) < ( F ` y ) ) )
118	112, 117, 100	rspcdva 2794	. . . . . . . . . 10 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> A. y e. ( A [,] B ) ( ( S - ( d / 2 ) ) < y -> ( F ` ( S - ( d / 2 ) ) ) < ( F ` y ) ) )
119	9	adantr 274	. . . . . . . . . 10 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> S e. ( A [,] B ) )
120	108, 118, 119	rspcdva 2794	. . . . . . . . 9 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( ( S - ( d / 2 ) ) < S -> ( F ` ( S - ( d / 2 ) ) ) < ( F ` S ) ) )
121	93, 120	mpd 13	. . . . . . . 8 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( F ` ( S - ( d / 2 ) ) ) < ( F ` S ) )
122	103, 104, 121	ltled 7881	. . . . . . 7 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( F ` ( S - ( d / 2 ) ) ) <_ ( F ` S ) )
123	103, 104, 122	abssuble0d 10949	. . . . . 6 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( abs ` ( ( F ` ( S - ( d / 2 ) ) ) - ( F ` S ) ) ) = ( ( F ` S ) - ( F ` ( S - ( d / 2 ) ) ) ) )
124	34	recnd 7794	. . . . . . . . . 10 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( S - ( d / 2 ) ) e. CC )
125	30	recnd 7794	. . . . . . . . . 10 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> S e. CC )
126	124, 125	abssubd 10965	. . . . . . . . 9 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( abs ` ( ( S - ( d / 2 ) ) - S ) ) = ( abs ` ( S - ( S - ( d / 2 ) ) ) ) )
127	33	recnd 7794	. . . . . . . . . . 11 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( d / 2 ) e. CC )
128	125, 127	nncand 8078	. . . . . . . . . 10 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( S - ( S - ( d / 2 ) ) ) = ( d / 2 ) )
129	128	fveq2d 5425	. . . . . . . . 9 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( abs ` ( S - ( S - ( d / 2 ) ) ) ) = ( abs ` ( d / 2 ) ) )
130	32	rpge0d 9487	. . . . . . . . . 10 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> 0 <_ ( d / 2 ) )
131	33, 130	absidd 10939	. . . . . . . . 9 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( abs ` ( d / 2 ) ) = ( d / 2 ) )
132	126, 129, 131	3eqtrd 2176	. . . . . . . 8 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( abs ` ( ( S - ( d / 2 ) ) - S ) ) = ( d / 2 ) )
133	132, 88	eqbrtrd 3950	. . . . . . 7 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( abs ` ( ( S - ( d / 2 ) ) - S ) ) < d )
134		fvoveq1 5797	. . . . . . . . . 10 |- ( z = ( S - ( d / 2 ) ) -> ( abs ` ( z - S ) ) = ( abs ` ( ( S - ( d / 2 ) ) - S ) ) )
135	134	breq1d 3939	. . . . . . . . 9 |- ( z = ( S - ( d / 2 ) ) -> ( ( abs ` ( z - S ) ) < d <-> ( abs ` ( ( S - ( d / 2 ) ) - S ) ) < d ) )
136	135	imbrov2fvoveq 5799	. . . . . . . 8 |- ( z = ( S - ( d / 2 ) ) -> ( ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) <-> ( ( abs ` ( ( S - ( d / 2 ) ) - S ) ) < d -> ( abs ` ( ( F ` ( S - ( d / 2 ) ) ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) )
137		simprr 521	. . . . . . . 8 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) )
138	2	adantr 274	. . . . . . . . 9 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( A [,] B ) C_ D )
139	138, 100	sseldd 3098	. . . . . . . 8 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( S - ( d / 2 ) ) e. D )
140	136, 137, 139	rspcdva 2794	. . . . . . 7 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( ( abs ` ( ( S - ( d / 2 ) ) - S ) ) < d -> ( abs ` ( ( F ` ( S - ( d / 2 ) ) ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) )
141	133, 140	mpd 13	. . . . . 6 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( abs ` ( ( F ` ( S - ( d / 2 ) ) ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) )
142	123, 141	eqbrtrrd 3952	. . . . 5 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( ( F ` S ) - ( F ` ( S - ( d / 2 ) ) ) ) < ( ( F ` S ) - U ) )
143	16	adantr 274	. . . . . 6 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> U e. RR )
144	143, 103, 104	ltsub2d 8317	. . . . 5 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( U < ( F ` ( S - ( d / 2 ) ) ) <-> ( ( F ` S ) - ( F ` ( S - ( d / 2 ) ) ) ) < ( ( F ` S ) - U ) ) )
145	142, 144	mpbird 166	. . . 4 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> U < ( F ` ( S - ( d / 2 ) ) ) )
146		fveq2 5421	. . . . . 6 |- ( w = ( S - ( d / 2 ) ) -> ( F ` w ) = ( F ` ( S - ( d / 2 ) ) ) )
147	146	breq2d 3941	. . . . 5 |- ( w = ( S - ( d / 2 ) ) -> ( U < ( F ` w ) <-> U < ( F ` ( S - ( d / 2 ) ) ) ) )
148	147, 6	elrab2 2843	. . . 4 |- ( ( S - ( d / 2 ) ) e. R <-> ( ( S - ( d / 2 ) ) e. ( A [,] B ) /\ U < ( F ` ( S - ( d / 2 ) ) ) ) )
149	100, 145, 148	sylanbrc 413	. . 3 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> ( S - ( d / 2 ) ) e. R )
150		breq1 3932	. . . 4 |- ( q = ( S - ( d / 2 ) ) -> ( q < S <-> ( S - ( d / 2 ) ) < S ) )
151	150	rspcev 2789	. . 3 |- ( ( ( S - ( d / 2 ) ) e. R /\ ( S - ( d / 2 ) ) < S ) -> E. q e. R q < S )
152	149, 93, 151	syl2anc 408	. 2 |- ( ( ph /\ ( d e. RR+ /\ A. z e. D ( ( abs ` ( z - S ) ) < d -> ( abs ` ( ( F ` z ) - ( F ` S ) ) ) < ( ( F ` S ) - U ) ) ) ) -> E. q e. R q < S )
153	23, 152	rexlimddv 2554	1 |- ( ph -> E. q e. R q < S )

Syntax hints:   -> wi 4   /\ wa 103   <-> wb 104   /\ w3a 962   = wceq 1331   e. wcel 1480   A.wral 2416   E.wrex 2417   {crab 2420   C_ wss 3071   class class class wbr 3929   ` cfv 5123  (class class class)co 5774   CCcc 7618   RRcr 7619   0cc0 7620   + caddc 7623   RR*cxr 7799   < clt 7800   <_ cle 7801   - cmin 7933   / cdiv 8432   2c2 8771   RR+crp 9441   [,]cicc 9674   abscabs 10769   -cn->ccncf 12726

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-ia1 105  ax-ia2 106  ax-ia3 107  ax-in1 603  ax-in2 604  ax-io 698  ax-5 1423  ax-7 1424  ax-gen 1425  ax-ie1 1469  ax-ie2 1470  ax-8 1482  ax-10 1483  ax-11 1484  ax-i12 1485  ax-bndl 1486  ax-4 1487  ax-13 1491  ax-14 1492  ax-17 1506  ax-i9 1510  ax-ial 1514  ax-i5r 1515  ax-ext 2121  ax-coll 4043  ax-sep 4046  ax-nul 4054  ax-pow 4098  ax-pr 4131  ax-un 4355  ax-setind 4452  ax-iinf 4502  ax-cnex 7711  ax-resscn 7712  ax-1cn 7713  ax-1re 7714  ax-icn 7715  ax-addcl 7716  ax-addrcl 7717  ax-mulcl 7718  ax-mulrcl 7719  ax-addcom 7720  ax-mulcom 7721  ax-addass 7722  ax-mulass 7723  ax-distr 7724  ax-i2m1 7725  ax-0lt1 7726  ax-1rid 7727  ax-0id 7728  ax-rnegex 7729  ax-precex 7730  ax-cnre 7731  ax-pre-ltirr 7732  ax-pre-ltwlin 7733  ax-pre-lttrn 7734  ax-pre-apti 7735  ax-pre-ltadd 7736  ax-pre-mulgt0 7737  ax-pre-mulext 7738  ax-arch 7739  ax-caucvg 7740

This theorem depends on definitions:  df-bi 116  df-dc 820  df-3or 963  df-3an 964  df-tru 1334  df-fal 1337  df-nf 1437  df-sb 1736  df-eu 2002  df-mo 2003  df-clab 2126  df-cleq 2132  df-clel 2135  df-nfc 2270  df-ne 2309  df-nel 2404  df-ral 2421  df-rex 2422  df-reu 2423  df-rmo 2424  df-rab 2425  df-v 2688  df-sbc 2910  df-csb 3004  df-dif 3073  df-un 3075  df-in 3077  df-ss 3084  df-nul 3364  df-if 3475  df-pw 3512  df-sn 3533  df-pr 3534  df-op 3536  df-uni 3737  df-int 3772  df-iun 3815  df-br 3930  df-opab 3990  df-mpt 3991  df-tr 4027  df-id 4215  df-po 4218  df-iso 4219  df-iord 4288  df-on 4290  df-ilim 4291  df-suc 4293  df-iom 4505  df-xp 4545  df-rel 4546  df-cnv 4547  df-co 4548  df-dm 4549  df-rn 4550  df-res 4551  df-ima 4552  df-iota 5088  df-fun 5125  df-fn 5126  df-f 5127  df-f1 5128  df-fo 5129  df-f1o 5130  df-fv 5131  df-riota 5730  df-ov 5777  df-oprab 5778  df-mpo 5779  df-1st 6038  df-2nd 6039  df-recs 6202  df-frec 6288  df-map 6544  df-pnf 7802  df-mnf 7803  df-xr 7804  df-ltxr 7805  df-le 7806  df-sub 7935  df-neg 7936  df-reap 8337  df-ap 8344  df-div 8433  df-inn 8721  df-2 8779  df-3 8780  df-4 8781  df-n0 8978  df-z 9055  df-uz 9327  df-rp 9442  df-icc 9678  df-seqfrec 10219  df-exp 10293  df-cj 10614  df-re 10615  df-im 10616  df-rsqrt 10770  df-abs 10771  df-cncf 12727

This theorem is referenced by:  ivthinclemur  12786