Description: Define the set size
function ♯, which gives the cardinality of a
finite set as a member of 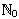 , and assigns all infinite sets the
value , and assigns all infinite sets the
value 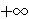 .
For example, .
For example, 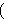 ♯ ♯ 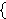 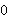  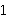  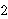  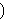 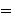 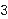 . .
Since we don't know that an arbitrary set is either finite or infinite
(by inffiexmid 7079), the behavior beyond finite sets is not as
useful as
it might appear. For example, we wouldn't expect to be able to define
this function in a meaningful way on 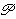 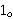 , which cannot be shown
to be finite (per pw1fin 7083). , which cannot be shown
to be finite (per pw1fin 7083).
Note that we use the sharp sign (♯) for this function and we use
the different character octothorpe (#) for the apartness
relation (see df-ap 8740). We adopt the former notation from
Corollary
8.2.4 of [AczelRathjen], p. 80
(although that work only defines it for
finite sets).
This definition (in terms of  and and 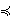 ) is not taken directly
from the literature, but for finite sets should be equivalent to the
conventional definition that the size of a finite set is the unique
natural number which is equinumerous to the given set. (Contributed by
Jim Kingdon, 19-Feb-2022.) ) is not taken directly
from the literature, but for finite sets should be equivalent to the
conventional definition that the size of a finite set is the unique
natural number which is equinumerous to the given set. (Contributed by
Jim Kingdon, 19-Feb-2022.) |