Theorem ceqsex8v 2901

Description: Elimination of eight existential quantifiers, using implicit substitution. (Contributed by NM, 23-Sep-2011.)

Hypotheses

Ref	Expression
ceqsex8v.1	|- A e. _V
ceqsex8v.2	|- B e. _V
ceqsex8v.3	|- C e. _V
ceqsex8v.4	|- D e. _V
ceqsex8v.5	|- E e. _V
ceqsex8v.6	|- F e. _V
ceqsex8v.7	|- G e. _V
ceqsex8v.8	|- H e. _V
ceqsex8v.9	|- (x = A -> (ph <-> ps))
ceqsex8v.10	|- (y = B -> (ps <-> ch))
ceqsex8v.11	|- (z = C -> (ch <-> th))
ceqsex8v.12	|- (w = D -> (th <-> ta))
ceqsex8v.13	|- (v = E -> (ta <-> et))
ceqsex8v.14	|- (u = F -> (et <-> ze))
ceqsex8v.15	|- (t = G -> (ze <-> si))
ceqsex8v.16	|- (s = H -> (si <-> rh))

Assertion

Ref	Expression
ceqsex8v	|- (E.xE.yE.zE.wE.vE.uE.tE.s(((x = A /\ y = B) /\ (z = C /\ w = D)) /\ ((v = E /\ u = F) /\ (t = G /\ s = H)) /\ ph) <-> rh)

Distinct variable groups:   x,y,z,w,v,u,t,s,A   x,B,y,z,w,v,u,t,s   x,C,y,z,w,v,u,t,s   x,D,y,z,w,v,u,t,s   x,E,y,z,w,v,u,t,s   x,F,y,z,w,v,u,t,s   x,G,y,z,w,v,u,t,s   x,H,y,z,w,v,u,t,s   ps,x   ch,y   th,z   ta,w   et,v   ze,u   si,t   rh,s

Allowed substitution hints:   ph(x,y,z,w,v,u,t,s)   ps(y,z,w,v,u,t,s)   ch(x,z,w,v,u,t,s)   th(x,y,w,v,u,t,s)   ta(x,y,z,v,u,t,s)   et(x,y,z,w,u,t,s)   ze(x,y,z,w,v,t,s)   si(x,y,z,w,v,u,s)   rh(x,y,z,w,v,u,t)

Proof of Theorem ceqsex8v

Step	Hyp	Ref	Expression
1		19.42vv 1907	. . . . . . 7 |- (E.tE.s(((x = A /\ y = B) /\ (z = C /\ w = D)) /\ ((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)) <-> (((x = A /\ y = B) /\ (z = C /\ w = D)) /\ E.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)))
2	1	2exbii 1583	. . . . . 6 |- (E.vE.uE.tE.s(((x = A /\ y = B) /\ (z = C /\ w = D)) /\ ((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)) <-> E.vE.u(((x = A /\ y = B) /\ (z = C /\ w = D)) /\ E.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)))
3		19.42vv 1907	. . . . . 6 |- (E.vE.u(((x = A /\ y = B) /\ (z = C /\ w = D)) /\ E.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)) <-> (((x = A /\ y = B) /\ (z = C /\ w = D)) /\ E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)))
4	2, 3	bitri 240	. . . . 5 |- (E.vE.uE.tE.s(((x = A /\ y = B) /\ (z = C /\ w = D)) /\ ((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)) <-> (((x = A /\ y = B) /\ (z = C /\ w = D)) /\ E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)))
5		3anass 938	. . . . . . . 8 |- ((((x = A /\ y = B) /\ (z = C /\ w = D)) /\ ((v = E /\ u = F) /\ (t = G /\ s = H)) /\ ph) <-> (((x = A /\ y = B) /\ (z = C /\ w = D)) /\ (((v = E /\ u = F) /\ (t = G /\ s = H)) /\ ph)))
6		df-3an 936	. . . . . . . . 9 |- (((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph) <-> (((v = E /\ u = F) /\ (t = G /\ s = H)) /\ ph))
7	6	anbi2i 675	. . . . . . . 8 |- ((((x = A /\ y = B) /\ (z = C /\ w = D)) /\ ((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)) <-> (((x = A /\ y = B) /\ (z = C /\ w = D)) /\ (((v = E /\ u = F) /\ (t = G /\ s = H)) /\ ph)))
8	5, 7	bitr4i 243	. . . . . . 7 |- ((((x = A /\ y = B) /\ (z = C /\ w = D)) /\ ((v = E /\ u = F) /\ (t = G /\ s = H)) /\ ph) <-> (((x = A /\ y = B) /\ (z = C /\ w = D)) /\ ((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)))
9	8	2exbii 1583	. . . . . 6 |- (E.tE.s(((x = A /\ y = B) /\ (z = C /\ w = D)) /\ ((v = E /\ u = F) /\ (t = G /\ s = H)) /\ ph) <-> E.tE.s(((x = A /\ y = B) /\ (z = C /\ w = D)) /\ ((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)))
10	9	2exbii 1583	. . . . 5 |- (E.vE.uE.tE.s(((x = A /\ y = B) /\ (z = C /\ w = D)) /\ ((v = E /\ u = F) /\ (t = G /\ s = H)) /\ ph) <-> E.vE.uE.tE.s(((x = A /\ y = B) /\ (z = C /\ w = D)) /\ ((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)))
11		df-3an 936	. . . . 5 |- (((x = A /\ y = B) /\ (z = C /\ w = D) /\ E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)) <-> (((x = A /\ y = B) /\ (z = C /\ w = D)) /\ E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)))
12	4, 10, 11	3bitr4i 268	. . . 4 |- (E.vE.uE.tE.s(((x = A /\ y = B) /\ (z = C /\ w = D)) /\ ((v = E /\ u = F) /\ (t = G /\ s = H)) /\ ph) <-> ((x = A /\ y = B) /\ (z = C /\ w = D) /\ E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)))
13	12	2exbii 1583	. . 3 |- (E.zE.wE.vE.uE.tE.s(((x = A /\ y = B) /\ (z = C /\ w = D)) /\ ((v = E /\ u = F) /\ (t = G /\ s = H)) /\ ph) <-> E.zE.w((x = A /\ y = B) /\ (z = C /\ w = D) /\ E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)))
14	13	2exbii 1583	. 2 |- (E.xE.yE.zE.wE.vE.uE.tE.s(((x = A /\ y = B) /\ (z = C /\ w = D)) /\ ((v = E /\ u = F) /\ (t = G /\ s = H)) /\ ph) <-> E.xE.yE.zE.w((x = A /\ y = B) /\ (z = C /\ w = D) /\ E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)))
15		ceqsex8v.1	. . . 4 |- A e. _V
16		ceqsex8v.2	. . . 4 |- B e. _V
17		ceqsex8v.3	. . . 4 |- C e. _V
18		ceqsex8v.4	. . . 4 |- D e. _V
19		ceqsex8v.9	. . . . . 6 |- (x = A -> (ph <-> ps))
20	19	3anbi3d 1258	. . . . 5 |- (x = A -> (((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph) <-> ((v = E /\ u = F) /\ (t = G /\ s = H) /\ ps)))
21	20	4exbidv 1630	. . . 4 |- (x = A -> (E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph) <-> E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ps)))
22		ceqsex8v.10	. . . . . 6 |- (y = B -> (ps <-> ch))
23	22	3anbi3d 1258	. . . . 5 |- (y = B -> (((v = E /\ u = F) /\ (t = G /\ s = H) /\ ps) <-> ((v = E /\ u = F) /\ (t = G /\ s = H) /\ ch)))
24	23	4exbidv 1630	. . . 4 |- (y = B -> (E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ps) <-> E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ch)))
25		ceqsex8v.11	. . . . . 6 |- (z = C -> (ch <-> th))
26	25	3anbi3d 1258	. . . . 5 |- (z = C -> (((v = E /\ u = F) /\ (t = G /\ s = H) /\ ch) <-> ((v = E /\ u = F) /\ (t = G /\ s = H) /\ th)))
27	26	4exbidv 1630	. . . 4 |- (z = C -> (E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ch) <-> E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ th)))
28		ceqsex8v.12	. . . . . 6 |- (w = D -> (th <-> ta))
29	28	3anbi3d 1258	. . . . 5 |- (w = D -> (((v = E /\ u = F) /\ (t = G /\ s = H) /\ th) <-> ((v = E /\ u = F) /\ (t = G /\ s = H) /\ ta)))
30	29	4exbidv 1630	. . . 4 |- (w = D -> (E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ th) <-> E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ta)))
31	15, 16, 17, 18, 21, 24, 27, 30	ceqsex4v 2899	. . 3 |- (E.xE.yE.zE.w((x = A /\ y = B) /\ (z = C /\ w = D) /\ E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)) <-> E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ta))
32		ceqsex8v.5	. . . 4 |- E e. _V
33		ceqsex8v.6	. . . 4 |- F e. _V
34		ceqsex8v.7	. . . 4 |- G e. _V
35		ceqsex8v.8	. . . 4 |- H e. _V
36		ceqsex8v.13	. . . 4 |- (v = E -> (ta <-> et))
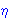37		ceqsex8v.14	. . . 4 |- (u = F -> (et <-> ze))
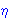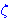38		ceqsex8v.15	. . . 4 |- (t = G -> (ze <-> si))
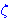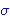39		ceqsex8v.16	. . . 4 |- (s = H -> (si <-> rh))
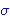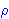40	32, 33, 34, 35, 36, 37, 38, 39	ceqsex4v 2899	. . 3 |- (E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ta) <-> rh)
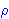41	31, 40	bitri 240	. 2 |- (E.xE.yE.zE.w((x = A /\ y = B) /\ (z = C /\ w = D) /\ E.vE.uE.tE.s((v = E /\ u = F) /\ (t = G /\ s = H) /\ ph)) <-> rh)
42	14, 41	bitri 240	1 |- (E.xE.yE.zE.wE.vE.uE.tE.s(((x = A /\ y = B) /\ (z = C /\ w = D)) /\ ((v = E /\ u = F) /\ (t = G /\ s = H)) /\ ph) <-> rh)

Syntax hints:   -> wi 4   <-> wb 176   /\ wa 358   /\ w3a 934  E.wex 1541   = wceq 1642   e. wcel 1710  _Vcvv 2860

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-3 8  ax-gen 1546  ax-5 1557  ax-17 1616  ax-9 1654  ax-8 1675  ax-6 1729  ax-7 1734  ax-11 1746  ax-ext 2334

This theorem depends on definitions:  df-bi 177  df-an 360  df-3an 936  df-tru 1319  df-ex 1542  df-nf 1545  df-sb 1649  df-clab 2340  df-cleq 2346  df-clel 2349  df-v 2862

This theorem is referenced by: (None)