Description: Axiom of Variable
Substitution. One of the 5 equality axioms of predicate
calculus. The final consequent 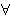      
  is a way of
expressing " is a way of
expressing " substituted for
substituted for  in wff in wff
 " (cf. sb6 1911).
It
is based on Lemma 16 of [Tarski] p. 70 and
Axiom C8 of [Monk2] p. 105,
from which it can be proved by cases. " (cf. sb6 1911).
It
is based on Lemma 16 of [Tarski] p. 70 and
Axiom C8 of [Monk2] p. 105,
from which it can be proved by cases.
Variants of this axiom which are equivalent in classical logic but which
have not been shown to be equivalent for intuitionistic logic are
ax11v 1851, ax11v2 1844 and ax-11o 1847. (Contributed by NM,
5-Aug-1993.) |