| Description: Axiom of Extensionality.
It states that two sets are identical if they
contain the same elements. Axiom 1 of [Crosilla] p. "Axioms of CZF and
IZF" (with unnecessary quantifiers removed).
Set theory can also be formulated with a single primitive
predicate
 on top of
traditional predicate calculus without equality. In
that case the Axiom of Extensionality becomes on top of
traditional predicate calculus without equality. In
that case the Axiom of Extensionality becomes
 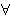 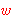  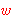    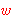    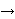     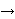      , and
equality , and
equality    is defined as is defined as 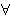 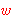  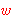   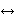 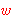
   . All
of the usual axioms of equality then become theorems of set theory.
See, for example, Axiom 1 of [TakeutiZaring] p. 8. . All
of the usual axioms of equality then become theorems of set theory.
See, for example, Axiom 1 of [TakeutiZaring] p. 8.
To use the above "equality-free" version of Extensionality
with
Metamath's logical axioms, we would rewrite ax-8 1528
through ax-16 1838 with
equality expanded according to the above definition. Some of those
axioms could be proved from set theory and would be redundant. Not all
of them are redundant, since our axioms of predicate calculus make
essential use of equality for the proper substitution that is a
primitive notion in traditional predicate calculus. A study of such an
axiomatization would be an interesting project for someone exploring the
foundations of logic.
It is important to understand that strictly speaking, all of our set
theory axioms are really schemes that represent an infinite number of
actual axioms. This is inherent in the design of Metamath
("metavariable math"), which manipulates only metavariables.
For
example, the metavariable  in ax-ext 2188 can represent any actual
variable v1, v2, v3,... . Distinct variable
restrictions ($d)
prevent us from substituting say v1 for both in ax-ext 2188 can represent any actual
variable v1, v2, v3,... . Distinct variable
restrictions ($d)
prevent us from substituting say v1 for both  and and  . This
is in contrast to typical textbook presentations that present actual
axioms (except for axioms which involve wff metavariables). In
practice, though, the theorems and proofs are essentially the same. The
$d restrictions make each of the infinite axioms generated by the
ax-ext 2188 scheme exactly logically equivalent to each
other and in
particular to the actual axiom of the textbook version. (Contributed by
NM, 5-Aug-1993.) . This
is in contrast to typical textbook presentations that present actual
axioms (except for axioms which involve wff metavariables). In
practice, though, the theorems and proofs are essentially the same. The
$d restrictions make each of the infinite axioms generated by the
ax-ext 2188 scheme exactly logically equivalent to each
other and in
particular to the actual axiom of the textbook version. (Contributed by
NM, 5-Aug-1993.) |