| Description: Axiom of Equality. One
of the equality and substitution axioms of
predicate calculus with equality. This is similar to, but not quite, a
transitive law for equality (proved later as equtr 1755). Axiom scheme C8'
in [Megill] p. 448 (p. 16 of the preprint).
Also appears as Axiom C7 of
[Monk2] p. 105.
Axioms ax-8 1550 through ax-16 1860 are the axioms having to do with equality,
substitution, and logical properties of our binary predicate 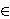 (which
later in set theory will mean "is a member of"). Note that all
axioms
except ax-16 1860 and ax-17 1572 are still valid even when (which
later in set theory will mean "is a member of"). Note that all
axioms
except ax-16 1860 and ax-17 1572 are still valid even when 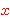 , ,  , and , and
 are replaced with
the same variable because they do not have any
distinct variable (Metamath's $d) restrictions. Distinct variable
restrictions are required for ax-16 1860 and ax-17 1572 only. (Contributed by
NM, 5-Aug-1993.) are replaced with
the same variable because they do not have any
distinct variable (Metamath's $d) restrictions. Distinct variable
restrictions are required for ax-16 1860 and ax-17 1572 only. (Contributed by
NM, 5-Aug-1993.) |