| Step | Hyp | Ref
| Expression |
|---|
| 1 | | df-sfin 4447 |
. . . 4
  Sfin Sfin          Nn Nn    Nn Nn      1 1 
          |
| 2 | | sfineq1 4527 |
. . . . . . 7
       Sfin Sfin       Sfin Sfin        |
| 3 | | eleq1 2413 |
. . . . . . . 8
         Spfin
Spfin    Spfin Spfin   |
| 4 | 3 | imbi2d 307 |
. . . . . . 7
        
 Spfin Spfin    Spfin Spfin      Spfin Spfin    Spfin Spfin    |
| 5 | 2, 4 | imbi12d 311 |
. . . . . 6
        Sfin Sfin        
 Spfin Spfin    Spfin Spfin  

 Sfin Sfin          Spfin Spfin    Spfin Spfin     |
| 6 | | sfineq2 4528 |
. . . . . . 7
       Sfin Sfin       Sfin Sfin        |
| 7 | | eleq1 2413 |
. . . . . . . 8
         Spfin
Spfin    Spfin Spfin   |
| 8 | 7 | imbi1d 308 |
. . . . . . 7
        
 Spfin Spfin    Spfin Spfin      Spfin Spfin    Spfin Spfin    |
| 9 | 6, 8 | imbi12d 311 |
. . . . . 6
        Sfin Sfin        
 Spfin Spfin    Spfin Spfin  

 Sfin Sfin          Spfin Spfin    Spfin Spfin     |
| 10 | | sfineq2 4528 |
. . . . . . . . . . . . . . 15
       Sfin Sfin       Sfin Sfin        |
| 11 | 10 | imbi1d 308 |
. . . . . . . . . . . . . 14
        Sfin Sfin        
    Sfin Sfin        
    |
| 12 | 11 | albidv 1625 |
. . . . . . . . . . . . 13
          Sfin Sfin               Sfin Sfin             |
| 13 | 12 | rspcv 2952 |
. . . . . . . . . . . 12
        
     Sfin Sfin               Sfin Sfin             |
| 14 | | sfineq1 4527 |
. . . . . . . . . . . . . . 15
       Sfin Sfin       Sfin Sfin        |
| 15 | | eleq1 2413 |
. . . . . . . . . . . . . . 15
        
       |
| 16 | 14, 15 | imbi12d 311 |
. . . . . . . . . . . . . 14
        Sfin Sfin        
    Sfin Sfin        
    |
| 17 | 16 | spv 1998 |
. . . . . . . . . . . . 13
     Sfin
Sfin             Sfin Sfin   
        |
| 18 | 17 | com12 27 |
. . . . . . . . . . . 12
  Sfin Sfin           Sfin Sfin
                |
| 19 | 13, 18 | syl9r 67 |
. . . . . . . . . . 11
  Sfin Sfin                    Sfin Sfin
                 |
| 20 | 19 | com23 72 |
. . . . . . . . . 10
  Sfin Sfin               Sfin Sfin
             
   
    |
| 21 | 20 | adantld 453 |
. . . . . . . . 9
  Sfin Sfin         Ncfin Ncfin       
    Sfin
Sfin                        |
| 22 | 21 | a2d 23 |
. . . . . . . 8
  Sfin Sfin          Ncfin Ncfin       
    Sfin
Sfin                    Ncfin Ncfin            Sfin Sfin
             
    |
| 23 | 22 | alimdv 1621 |
. . . . . . 7
  Sfin Sfin            Ncfin Ncfin   
    
   Sfin Sfin        
             Ncfin
Ncfin       
    Sfin
Sfin                   |
| 24 | | df-spfin 4448 |
. . . . . . . . 9
 Spfin Spfin  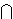     Ncfin Ncfin   
    
   Sfin Sfin        
    |
| 25 | 24 | eleq2i 2417 |
. . . . . . . 8
    Spfin Spfin    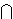     Ncfin Ncfin
           Sfin Sfin
             |
| 26 | | vex 2863 |
. . . . . . . . 9
    |
| 27 | 26 | elintab 3938 |
. . . . . . . 8
    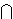     Ncfin
Ncfin       
    Sfin
Sfin                  Ncfin
Ncfin       
    Sfin
Sfin                  |
| 28 | 25, 27 | bitri 240 |
. . . . . . 7
    Spfin Spfin      Ncfin
Ncfin       
    Sfin
Sfin                  |
| 29 | 24 | eleq2i 2417 |
. . . . . . . 8
    Spfin Spfin    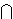     Ncfin Ncfin
           Sfin Sfin
             |
| 30 | | vex 2863 |
. . . . . . . . 9
    |
| 31 | 30 | elintab 3938 |
. . . . . . . 8
    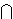     Ncfin
Ncfin       
    Sfin
Sfin                  Ncfin
Ncfin       
    Sfin
Sfin                  |
| 32 | 29, 31 | bitri 240 |
. . . . . . 7
    Spfin Spfin      Ncfin
Ncfin       
    Sfin
Sfin                  |
| 33 | 23, 28, 32 | 3imtr4g 261 |
. . . . . 6
  Sfin Sfin          Spfin Spfin    Spfin Spfin   |
| 34 | 5, 9, 33 | vtocl2g 2919 |
. . . . 5
     Nn Nn    Nn Nn    Sfin Sfin          Spfin Spfin    Spfin Spfin    |
| 35 | 34 | 3adant3 975 |
. . . 4
     Nn Nn    Nn Nn      1 1 
        
  Sfin Sfin          Spfin Spfin    Spfin Spfin    |
| 36 | 1, 35 | sylbi 187 |
. . 3
  Sfin Sfin        Sfin Sfin   
      Spfin Spfin    Spfin Spfin    |
| 37 | 36 | pm2.43i 43 |
. 2
  Sfin Sfin          Spfin Spfin    Spfin Spfin   |
| 38 | 37 | impcom 419 |
1
     Spfin Spfin  Sfin Sfin          Spfin Spfin  |