Description: Definition of the
conditional operator for propositions. The expression
if-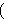    
 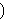 is read "if is read "if  then then  else else  ".
See dfifp2dc 987, dfifp3dc 988, dfifp4dc 989 and dfifp5dc 990 for alternate
definitions. ".
See dfifp2dc 987, dfifp3dc 988, dfifp4dc 989 and dfifp5dc 990 for alternate
definitions.
This definition (in the form of dfifp2dc 987) appears in Section II.24 of
[Church] p. 129 (Definition D12 page 132),
where it is called "conditioned
disjunction". Church's 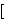      ![] ]](rbrack.gif) corresponds to our
if-
corresponds to our
if-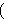    
 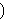 (note the permutation of the first two
variables). (note the permutation of the first two
variables).
This form was chosen as the definition rather than dfifp2dc 987 for
compatibility with intuitionistic logic development: with this form, it is
clear that if-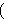    
 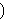 implies decidability of implies decidability of  (ifpdc 985), which is most often what is wanted.
(ifpdc 985), which is most often what is wanted.
(Contributed by BJ, 22-Jun-2019.) |