Description: Define the sum of a
series with an index set of integers  . The
variable . The
variable  is
normally a free variable in is
normally a free variable in 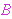 , i.e., , i.e., 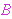 can
be
thought of as can
be
thought of as 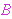    . This definition is the result of a
collection of discussions over the most general definition for a sum
that does not need the index set to have a specified ordering. This
definition is in two parts, one for finite sums and one for subsets of
the upper integers. When summing over a subset of the upper integers,
we extend the index set to the upper integers by adding zero outside the
domain, and then sum the set in order, setting the result to the limit
of the partial sums, if it exists. This means that conditionally
convergent sums can be evaluated meaningfully. For finite sums, we are
explicitly order-independent, by picking any bijection to a 1-based
finite sequence and summing in the induced order. In both cases we have
an . This definition is the result of a
collection of discussions over the most general definition for a sum
that does not need the index set to have a specified ordering. This
definition is in two parts, one for finite sums and one for subsets of
the upper integers. When summing over a subset of the upper integers,
we extend the index set to the upper integers by adding zero outside the
domain, and then sum the set in order, setting the result to the limit
of the partial sums, if it exists. This means that conditionally
convergent sums can be evaluated meaningfully. For finite sums, we are
explicitly order-independent, by picking any bijection to a 1-based
finite sequence and summing in the induced order. In both cases we have
an 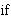 expression so that we only need
expression so that we only need 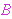 to be defined where to be defined where
   . In the infinite case, we also require
that the indexing
set be a decidable subset of an upperset of integers (that is,
membership of integers in it is decidable). These two methods of
summation produce the same result on their common region of definition
(i.e., finite sets of integers). Examples: . In the infinite case, we also require
that the indexing
set be a decidable subset of an upperset of integers (that is,
membership of integers in it is decidable). These two methods of
summation produce the same result on their common region of definition
(i.e., finite sets of integers). Examples:
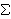   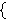 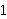  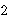  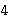 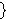  means means 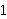 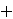 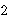 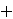 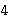  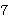 , and , and
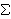   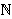  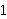 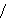  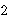 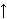     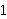 means 1/2 + 1/4 + 1/8 + ... = 1
(geoihalfsum 11918). (Contributed by NM, 11-Dec-2005.)
(Revised by Jim
Kingdon, 21-May-2023.) means 1/2 + 1/4 + 1/8 + ... = 1
(geoihalfsum 11918). (Contributed by NM, 11-Dec-2005.)
(Revised by Jim
Kingdon, 21-May-2023.) |