| Description: Double negation of
decidability of a formula. Intuitionistic logic
refutes the negation of decidability (but does not prove decidability) of
any formula.
This should not trick the reader into thinking that   EXMID is
provable in intuitionistic logic. Indeed, if we could quantify over
formula metavariables, then generalizing nnexmid 852 over EXMID is
provable in intuitionistic logic. Indeed, if we could quantify over
formula metavariables, then generalizing nnexmid 852 over  would
give " would
give "
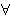    DECID DECID  ", but EXMID
is " ", but EXMID
is "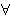  DECID DECID  ", so proving ", so proving   EXMID would amount to
proving "
EXMID would amount to
proving "
 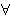  DECID DECID  ", which is not
implied by the above
theorem. Indeed, the converse of nnal 1673 does not hold. Since our system
does not allow quantification over formula metavariables, we can reproduce
this argument by representing formulas as subsets of ", which is not
implied by the above
theorem. Indeed, the converse of nnal 1673 does not hold. Since our system
does not allow quantification over formula metavariables, we can reproduce
this argument by representing formulas as subsets of 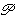 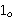 , like we
do in our definition of EXMID (df-exmid 4255): then, we can prove , like we
do in our definition of EXMID (df-exmid 4255): then, we can prove
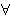   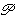 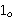   DECID DECID   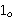 but we cannot prove
but we cannot prove
  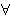  
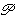 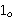 DECID DECID   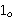 because the converse of nnral 2498 does
not hold.
because the converse of nnral 2498 does
not hold.
Actually, 
 EXMID is not provable in intuitionistic logic since
intuitionistic logic has models satisfying
EXMID is not provable in intuitionistic logic since
intuitionistic logic has models satisfying  EXMID and
noncontradiction holds (pm3.24 695). (Contributed by BJ, 9-Oct-2019.)
Add explanation on non-provability of EXMID and
noncontradiction holds (pm3.24 695). (Contributed by BJ, 9-Oct-2019.)
Add explanation on non-provability of   EXMID. (Revised by BJ,
11-Aug-2024.) EXMID. (Revised by BJ,
11-Aug-2024.) |