| Description: The expression
EXMID will be used as a readable shorthand for any
form of the law of the excluded middle; this is a useful shorthand
largely because it hides statements of the form "for any
proposition" in
a system which can only quantify over sets, not propositions.
To see how this compares with other ways of expressing excluded middle,
compare undifexmid 4222 with exmidundif 4235. The former may be more
recognizable as excluded middle because it is in terms of propositions,
and the proof may be easier to follow for much the same reason (it just
has to show  and 
in the the
relevant parts of the
proof). The latter, however, has the key advantage of being able to
prove both directions of the biconditional. To state that excluded
middle implies a proposition is hard to do gracefully without
EXMID, because there is no way to write a hypothesis
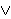 for an arbitrary proposition; instead the
hypothesis
would need to be the particular instance of excluded middle which that
proof needs. Or to say it another way, EXMID implies
DECID
by exmidexmid 4225 but there is no good way to express the
converse.
This definition and how we use it is easiest to understand (and most
appropriate to assign the name "excluded middle" to) if we
assume
ax-sep 4147, in which case EXMID means
that all propositions are
decidable (see exmidexmid 4225 and notice that it relies on ax-sep 4147). If
we instead work with ax-bdsep 15376, EXMID as defined
here means that
all bounded propositions are decidable.
(Contributed by Mario Carneiro and Jim Kingdon,
18-Jun-2022.) |
EXMID 
DECID 
EXMID
