Theorem xordidc 1410

Description: Conjunction distributes over exclusive-or, for decidable propositions. This is one way to interpret the distributive law of multiplication over addition in modulo 2 arithmetic. (Contributed by Jim Kingdon, 14-Jul-2018.)

Assertion

Ref	Expression
xordidc	|- (DECID ph -> (DECID ps -> (DECID ch -> ( ( ph /\ ( ps \/_ ch ) ) <-> ( ( ph /\ ps ) \/_ ( ph /\ ch ) ) ) ) ) )

Proof of Theorem xordidc

Step	Hyp	Ref	Expression
1		dcbi 938	. . . . 5 |- (DECID ps -> (DECID ch -> DECID ( ps <-> ch ) ) )
2	1	imp 124	. . . 4 |- ( (DECID ps /\ DECID ch ) -> DECID ( ps <-> ch ) )
3		annimdc 939	. . . . . 6 |- (DECID ph -> (DECID ( ps <-> ch ) -> ( ( ph /\ -. ( ps <-> ch ) ) <-> -. ( ph -> ( ps <-> ch ) ) ) ) )
4	3	imp 124	. . . . 5 |- ( (DECID ph /\ DECID ( ps <-> ch ) ) -> ( ( ph /\ -. ( ps <-> ch ) ) <-> -. ( ph -> ( ps <-> ch ) ) ) )
5		pm5.32 453	. . . . . 6 |- ( ( ph -> ( ps <-> ch ) ) <-> ( ( ph /\ ps ) <-> ( ph /\ ch ) ) )
6	5	notbii 669	. . . . 5 |- ( -. ( ph -> ( ps <-> ch ) ) <-> -. ( ( ph /\ ps ) <-> ( ph /\ ch ) ) )
7	4, 6	bitrdi 196	. . . 4 |- ( (DECID ph /\ DECID ( ps <-> ch ) ) -> ( ( ph /\ -. ( ps <-> ch ) ) <-> -. ( ( ph /\ ps ) <-> ( ph /\ ch ) ) ) )
8	2, 7	sylan2 286	. . 3 |- ( (DECID ph /\ (DECID ps /\ DECID ch ) ) -> ( ( ph /\ -. ( ps <-> ch ) ) <-> -. ( ( ph /\ ps ) <-> ( ph /\ ch ) ) ) )
9		xornbidc 1402	. . . . . 6 |- (DECID ps -> (DECID ch -> ( ( ps \/_ ch ) <-> -. ( ps <-> ch ) ) ) )
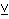
10	9	imp 124	. . . . 5 |- ( (DECID ps /\ DECID ch ) -> ( ( ps \/_ ch ) <-> -. ( ps <-> ch ) ) )
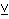
11	10	adantl 277	. . . 4 |- ( (DECID ph /\ (DECID ps /\ DECID ch ) ) -> ( ( ps \/_ ch ) <-> -. ( ps <-> ch ) ) )
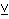
12	11	anbi2d 464	. . 3 |- ( (DECID ph /\ (DECID ps /\ DECID ch ) ) -> ( ( ph /\ ( ps \/_ ch ) ) <-> ( ph /\ -. ( ps <-> ch ) ) ) )
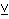
13		dcan 935	. . . . 5 |- ( (DECID ph /\ DECID ps ) -> DECID ( ph /\ ps ) )
14	13	adantrr 479	. . . 4 |- ( (DECID ph /\ (DECID ps /\ DECID ch ) ) -> DECID ( ph /\ ps ) )
15		dcan 935	. . . . 5 |- ( (DECID ph /\ DECID ch ) -> DECID ( ph /\ ch ) )
16	15	adantrl 478	. . . 4 |- ( (DECID ph /\ (DECID ps /\ DECID ch ) ) -> DECID ( ph /\ ch ) )
17		xornbidc 1402	. . . 4 |- (DECID ( ph /\ ps ) -> (DECID ( ph /\ ch ) -> ( ( ( ph /\ ps ) \/_ ( ph /\ ch ) ) <-> -. ( ( ph /\ ps ) <-> ( ph /\ ch ) ) ) ) )
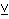
18	14, 16, 17	sylc 62	. . 3 |- ( (DECID ph /\ (DECID ps /\ DECID ch ) ) -> ( ( ( ph /\ ps ) \/_ ( ph /\ ch ) ) <-> -. ( ( ph /\ ps ) <-> ( ph /\ ch ) ) ) )
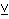
19	8, 12, 18	3bitr4d 220	. 2 |- ( (DECID ph /\ (DECID ps /\ DECID ch ) ) -> ( ( ph /\ ( ps \/_ ch ) ) <-> ( ( ph /\ ps ) \/_ ( ph /\ ch ) ) ) )
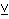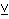20	19	exp32 365	1 |- (DECID ph -> (DECID ps -> (DECID ch -> ( ( ph /\ ( ps \/_ ch ) ) <-> ( ( ph /\ ps ) \/_ ( ph /\ ch ) ) ) ) ) )

Syntax hints:   -. wn 3   -> wi 4   /\ wa 104   <-> wb 105  DECID wdc 835   \/_ wxo 1386

This theorem was proved from axioms:  ax-mp 5  ax-1 6  ax-2 7  ax-ia1 106  ax-ia2 107  ax-ia3 108  ax-in1 615  ax-in2 616  ax-io 710

This theorem depends on definitions:  df-bi 117  df-stab 832  df-dc 836  df-xor 1387

This theorem is referenced by: (None)