| Description: Equality of a class
variable and a class abstraction (also called a
class builder). Theorem 5.1 of [Quine] p.
34. This theorem shows the
relationship between expressions with class abstractions and expressions
with class variables. Note that abbi 2464 and its relatives are among
those useful for converting theorems with class variables to equivalent
theorems with wff variables, by first substituting a class abstraction
for each class variable.
Class variables can always be eliminated from a theorem to result in an
equivalent theorem with wff variables, and vice-versa. The idea is
roughly as follows. To convert a theorem with a wff variable  (that has a free variable
(that has a free variable 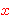 ) to a theorem with a class variable ) to a theorem with a class variable
 , we
substitute , we
substitute 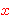 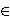  for for  throughout and simplify,
where throughout and simplify,
where  is a
new class variable not already in the wff. An example
is the conversion of zfauscl in set.mm to inex1 in set.mm (look at the
instance of zfauscl that occurs in the proof of inex1 ). Conversely, to
convert a theorem with a class variable is a
new class variable not already in the wff. An example
is the conversion of zfauscl in set.mm to inex1 in set.mm (look at the
instance of zfauscl that occurs in the proof of inex1 ). Conversely, to
convert a theorem with a class variable  to one with to one with  , we
substitute , we
substitute 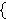 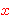    for for  throughout and simplify, where throughout and simplify, where 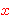 and
and  are
new setvar and wff variables not already in the wff. An
example is cp in set.mm , which derives a formula containing wff
variables from substitution instances of the class variables in its
equivalent formulation cplem2 in set.mm. For more information on class
variables, see Quine pp. 15-21 and/or Takeuti and Zaring pp. 10-13.
(Contributed by NM, 5-Aug-1993.) are
new setvar and wff variables not already in the wff. An
example is cp in set.mm , which derives a formula containing wff
variables from substitution instances of the class variables in its
equivalent formulation cplem2 in set.mm. For more information on class
variables, see Quine pp. 15-21 and/or Takeuti and Zaring pp. 10-13.
(Contributed by NM, 5-Aug-1993.) |