| Step | Hyp | Ref
| Expression |
|---|
| 1 | | nncex 4397 |
. . 3
 Nn Nn   |
| 2 | | inexg 4101 |
. . 3
   Nn Nn          Nn Nn   
   |
| 3 | 1, 2 | mpan 651 |
. 2
       Nn Nn    
  |
| 4 | | peano1 4403 |
. . 3
 0c
0c  Nn
Nn |
| 5 | | elin 3220 |
. . . 4
  0c 0c   Nn Nn      0c 0c  Nn Nn  0c 0c     |
| 6 | 5 | biimpri 197 |
. . 3
   0c 0c  Nn Nn  0c 0c
    0c 0c   Nn Nn     |
| 7 | 4, 6 | mpan 651 |
. 2
  0c 0c    0c 0c   Nn Nn     |
| 8 | | elin 3220 |
. . . . . 6
     Nn Nn        Nn Nn       |
| 9 | 8 | imbi1i 315 |
. . . . 5
      Nn Nn      
 1c
1c
        Nn Nn          1c 1c     |
| 10 | | impexp 433 |
. . . . 5
      Nn Nn          1c 1c        Nn Nn          1c
1c
     |
| 11 | 9, 10 | bitri 240 |
. . . 4
      Nn Nn      
 1c
1c
       Nn Nn          1c 1c 
    |
| 12 | | inss1 3476 |
. . . . . . . 8
  Nn Nn     Nn Nn |
| 13 | 12 | sseli 3270 |
. . . . . . 7
     Nn Nn       Nn
Nn  |
| 14 | | peano2 4404 |
. . . . . . 7
    Nn Nn     1c
1c
 Nn Nn  |
| 15 | 13, 14 | syl 15 |
. . . . . 6
     Nn Nn      
 1c
1c
 Nn Nn  |
| 16 | | elin 3220 |
. . . . . . . 8
     1c
1c
  Nn Nn         1c 1c  Nn Nn   
 1c
1c
    |
| 17 | 16 | biimpri 197 |
. . . . . . 7
      1c
1c
 Nn Nn     1c 1c        1c 1c   Nn Nn     |
| 18 | 17 | a1i 10 |
. . . . . 6
     Nn Nn          1c 1c  Nn Nn   
 1c
1c
       1c 1c   Nn
Nn      |
| 19 | 15, 18 | mpand 656 |
. . . . 5
     Nn Nn         1c
1c
      1c
1c
  Nn Nn      |
| 20 | 19 | a2i 12 |
. . . 4
      Nn Nn      
 1c
1c
        Nn Nn   
    1c 1c   Nn Nn      |
| 21 | 11, 20 | sylbir 204 |
. . 3
     Nn Nn          1c 1c 
        Nn Nn   
    1c 1c   Nn Nn      |
| 22 | 21 | ralimi2 2687 |
. 2
     Nn
Nn         1c
1c
        Nn Nn       1c 1c   Nn
Nn     |
| 23 | | df-nnc 4380 |
. . . 4
 Nn Nn  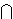     0c 0c      
    1c 1c     |
| 24 | | eleq2 2414 |
. . . . . . . . 9
     Nn Nn      0c 0c  
 0c
0c 
 Nn Nn      |
| 25 | | eleq2 2414 |
. . . . . . . . . 10
     Nn Nn         1c
1c
    
 1c
1c
  Nn Nn      |
| 26 | 25 | raleqbi1dv 2816 |
. . . . . . . . 9
     Nn Nn             1c
1c
    
  Nn Nn       1c
1c
  Nn Nn      |
| 27 | 24, 26 | anbi12d 691 |
. . . . . . . 8
     Nn Nn       0c 0c      
    1c 1c      0c 0c   Nn Nn         Nn Nn       1c
1c
  Nn Nn       |
| 28 | 27 | elabg 2987 |
. . . . . . 7
   Nn Nn    
    Nn
Nn       
 0c 0c
          1c
1c
      0c 0c   Nn Nn         Nn Nn       1c
1c
  Nn Nn       |
| 29 | 28 | biimprd 214 |
. . . . . 6
   Nn Nn    
    0c 0c   Nn Nn         Nn Nn       1c
1c
  Nn Nn    
  Nn Nn    
    0c 0c      
    1c 1c       |
| 30 | 29 | 3impib 1149 |
. . . . 5
    Nn Nn   
   0c 0c   Nn Nn   
     Nn
Nn       1c 1c 
 Nn Nn       Nn Nn   
     0c 0c      
    1c 1c      |
| 31 | | intss1 3942 |
. . . . 5
   Nn Nn    
    0c 0c      
    1c 1c      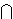   
 0c 0c
          1c
1c
    
 Nn Nn     |
| 32 | 30, 31 | syl 15 |
. . . 4
    Nn Nn   
   0c 0c   Nn Nn   
     Nn
Nn       1c 1c 
 Nn Nn      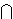     0c 0c      
    1c 1c     
 Nn Nn     |
| 33 | 23, 32 | syl5eqss 3316 |
. . 3
    Nn Nn   
   0c 0c   Nn Nn   
     Nn
Nn       1c 1c 
 Nn Nn      Nn Nn   Nn Nn     |
| 34 | | inss2 3477 |
. . 3
  Nn Nn      |
| 35 | 33, 34 | syl6ss 3285 |
. 2
    Nn Nn   
   0c 0c   Nn Nn   
     Nn
Nn       1c 1c 
 Nn Nn      Nn Nn    |
| 36 | 3, 7, 22, 35 | syl3an 1224 |
1
       0c 0c       Nn Nn         1c 1c      Nn Nn    |