Proof of Theorem nncex
| Step | Hyp | Ref
| Expression |
|---|
| 1 | | dfnnc2 4396 |
. 2
 Nn Nn  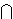     0c
0c 
     Sk Sk   Sk Sk  k SIk Imagek k SIk Imagek  Ins3k ∼ Ins3k ∼   Ins3k Sk Ins3k Sk  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    Ins2k Ins2k Sk Ins2k Ins2k Sk   Ins2k Ins3k Sk Ins2k Ins3k Sk  Ins3k SIk SIk Sk Ins3k SIk SIk Sk    k k 1 1  1 1  1 1  1 1c 1 1c   k k 1 1  1 1c 1 1c    k1c k1c  |
| 2 | | setswithex 4323 |
. . . 4
    0c 0c      |
| 3 | | ssetkex 4295 |
. . . . . 6
 Sk Sk   |
| 4 | | addcexlem 4383 |
. . . . . . . . . 10
  Ins3k ∼ Ins3k ∼   Ins3k Sk Ins3k Sk  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    Ins2k Ins2k Sk Ins2k Ins2k Sk   Ins2k Ins3k Sk Ins2k Ins3k Sk  Ins3k SIk SIk Sk Ins3k SIk SIk Sk    k k 1 1  1 1  1 1  1 1c 1 1c 
  |
| 5 | | 1cex 4143 |
. . . . . . . . . . . 12
 1c
1c 
 |
| 6 | 5 | pw1ex 4304 |
. . . . . . . . . . 11
  1
1c 1
1c 
 |
| 7 | 6 | pw1ex 4304 |
. . . . . . . . . 10
  1 1  1
1c 1
1c 
 |
| 8 | 4, 7 | imakex 4301 |
. . . . . . . . 9
   Ins3k ∼ Ins3k ∼   Ins3k Sk Ins3k Sk  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    Ins2k Ins2k Sk Ins2k Ins2k Sk   Ins2k Ins3k Sk Ins2k Ins3k Sk  Ins3k SIk SIk Sk Ins3k SIk SIk Sk    k k 1 1  1 1  1 1  1 1c 1 1c   k k 1 1  1 1c 1 1c 
 |
| 9 | 8 | imagekex 4313 |
. . . . . . . 8
 Imagek
Imagek  Ins3k ∼ Ins3k ∼   Ins3k Sk Ins3k Sk  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    Ins2k Ins2k Sk Ins2k Ins2k Sk   Ins2k Ins3k Sk Ins2k Ins3k Sk  Ins3k SIk SIk Sk Ins3k SIk SIk Sk    k k 1 1  1 1  1 1  1 1c 1 1c   k k 1 1  1 1c 1 1c 
 |
| 10 | 9 | sikex 4298 |
. . . . . . 7
 SIk Imagek SIk Imagek  Ins3k ∼ Ins3k ∼   Ins3k Sk Ins3k Sk  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    Ins2k Ins2k Sk Ins2k Ins2k Sk   Ins2k Ins3k Sk Ins2k Ins3k Sk  Ins3k SIk SIk Sk Ins3k SIk SIk Sk    k k 1 1  1 1  1 1  1 1c 1 1c   k k 1 1  1 1c 1 1c 
 |
| 11 | 3, 10 | cokex 4311 |
. . . . . 6
  Sk Sk  k SIk Imagek k SIk Imagek  Ins3k ∼ Ins3k ∼   Ins3k Sk Ins3k Sk  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    Ins2k Ins2k Sk Ins2k Ins2k Sk   Ins2k Ins3k Sk Ins2k Ins3k Sk  Ins3k SIk SIk Sk Ins3k SIk SIk Sk    k k 1 1  1 1  1 1  1 1c 1 1c   k k 1 1  1 1c 1 1c 
  |
| 12 | 3, 11 | difex 4108 |
. . . . 5
  Sk Sk   Sk Sk  k SIk Imagek k SIk Imagek  Ins3k ∼ Ins3k ∼   Ins3k Sk Ins3k Sk  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    Ins2k Ins2k Sk Ins2k Ins2k Sk   Ins2k Ins3k Sk Ins2k Ins3k Sk  Ins3k SIk SIk Sk Ins3k SIk SIk Sk    k k 1 1  1 1  1 1  1 1c 1 1c   k k 1 1  1 1c 1 1c     |
| 13 | 12, 5 | imakex 4301 |
. . . 4
   Sk Sk   Sk Sk  k SIk Imagek k SIk Imagek  Ins3k ∼ Ins3k ∼   Ins3k Sk Ins3k Sk  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    Ins2k Ins2k Sk Ins2k Ins2k Sk   Ins2k Ins3k Sk Ins2k Ins3k Sk  Ins3k SIk SIk Sk Ins3k SIk SIk Sk    k k 1 1  1 1  1 1  1 1c 1 1c   k k 1 1  1 1c 1 1c    k1c k1c   |
| 14 | 2, 13 | difex 4108 |
. . 3
     0c
0c 
     Sk Sk   Sk Sk  k SIk Imagek k SIk Imagek  Ins3k ∼ Ins3k ∼   Ins3k Sk Ins3k Sk  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    Ins2k Ins2k Sk Ins2k Ins2k Sk   Ins2k Ins3k Sk Ins2k Ins3k Sk  Ins3k SIk SIk Sk Ins3k SIk SIk Sk    k k 1 1  1 1  1 1  1 1c 1 1c   k k 1 1  1 1c 1 1c    k1c k1c    |
| 15 | 14 | intex 4321 |
. 2
 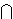   
 0c 0c
      Sk Sk   Sk Sk  k SIk Imagek k SIk Imagek  Ins3k ∼ Ins3k ∼   Ins3k Sk Ins3k Sk  Ins2k Sk Ins2k Sk   k k 1 1  1 1c 1 1c    Ins2k Ins2k Sk Ins2k Ins2k Sk   Ins2k Ins3k Sk Ins2k Ins3k Sk  Ins3k SIk SIk Sk Ins3k SIk SIk Sk    k k 1 1  1 1  1 1  1 1c 1 1c   k k 1 1  1 1c 1 1c    k1c k1c    |
| 16 | 1, 15 | eqeltri 2423 |
1
 Nn Nn   |