Description: Definition of an ordered
pair, equivalent to Kuratowski's definition
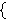 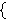  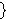 
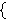   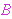 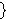 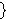 when the arguments are
sets. Since the
behavior of Kuratowski definition is not very useful for proper classes,
we define it to be empty in this case (see opprc1 3855 and opprc2 3856). For
Kuratowski's actual definition when the arguments are sets, see dfop 3832. when the arguments are
sets. Since the
behavior of Kuratowski definition is not very useful for proper classes,
we define it to be empty in this case (see opprc1 3855 and opprc2 3856). For
Kuratowski's actual definition when the arguments are sets, see dfop 3832.
Definition 9.1 of [Quine] p. 58 defines an
ordered pair unconditionally
as 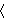   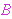 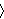  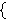 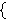  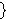 
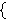   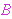 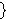  , which has different
behavior from our df-op 3652 when the arguments are proper classes.
Ordinarily this difference is not important, since neither definition is
meaningful in that case. Our df-op 3652 was chosen because it often makes
proofs shorter by eliminating unnecessary sethood hypotheses. , which has different
behavior from our df-op 3652 when the arguments are proper classes.
Ordinarily this difference is not important, since neither definition is
meaningful in that case. Our df-op 3652 was chosen because it often makes
proofs shorter by eliminating unnecessary sethood hypotheses.
There are other ways to define ordered pairs. The basic requirement is
that two ordered pairs are equal iff their respective members are equal.
In 1914 Norbert Wiener gave the first successful definition
   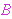  2 2  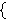 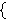 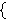  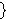 
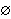 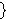  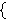 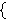 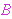 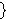 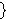 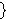 . This was
simplified by Kazimierz Kuratowski in 1921 to our present definition.
An even simpler definition is . This was
simplified by Kazimierz Kuratowski in 1921 to our present definition.
An even simpler definition is 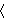   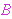 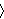 3 3
 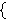   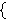   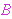 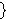 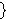 ,
but it requires the Axiom of Regularity for
its justification and is not commonly used. Finally, an ordered pair of
real numbers can be represented by a complex number. (Contributed by
NM, 28-May-1995.) (Revised by Mario Carneiro,
26-Apr-2015.) ,
but it requires the Axiom of Regularity for
its justification and is not commonly used. Finally, an ordered pair of
real numbers can be represented by a complex number. (Contributed by
NM, 28-May-1995.) (Revised by Mario Carneiro,
26-Apr-2015.) |